Question

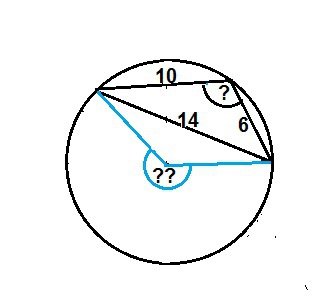
Треугольник со сторонами 6, 10 и 14 см вписан в окружность. найдите центральный угол, соответственно вписанный углу, образованому двумя меньшими сторонами треугольника.

Answer 1

Треугольник вписан в окружность, следовательно, все его вершины расположены на окружности и все углы вписанные. Центральный угол, опирающийся на ту же дугу, что вписанный, в два раза больше его ( свойство).
Найти угол треугольника, если известны все его стороны, можно по т.косинусов:
 Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Ищем угол между сторонами 6 и 10.  Пусть это угол α.
Тогда 
14²=6²+10²-2•6•10•cos∠α
196=36+100-120•cos∠α⇒
60=-120₽•cos∠α
cos∠α= -1/2.
Отрицательный косинус - это косинус тупого угла 120°⇒
центральный угол, опирающийся на ту же дугу, что вписанный угол величиной 120°, равен
120°•2=240°