Предмет: Экономика,
автор: andrejkn
99 баллов.
Помогите пожалуйста решить графически задачу линейного
программирования.(подробно)
Пример приведен на фото 2 и 3
Приложения:
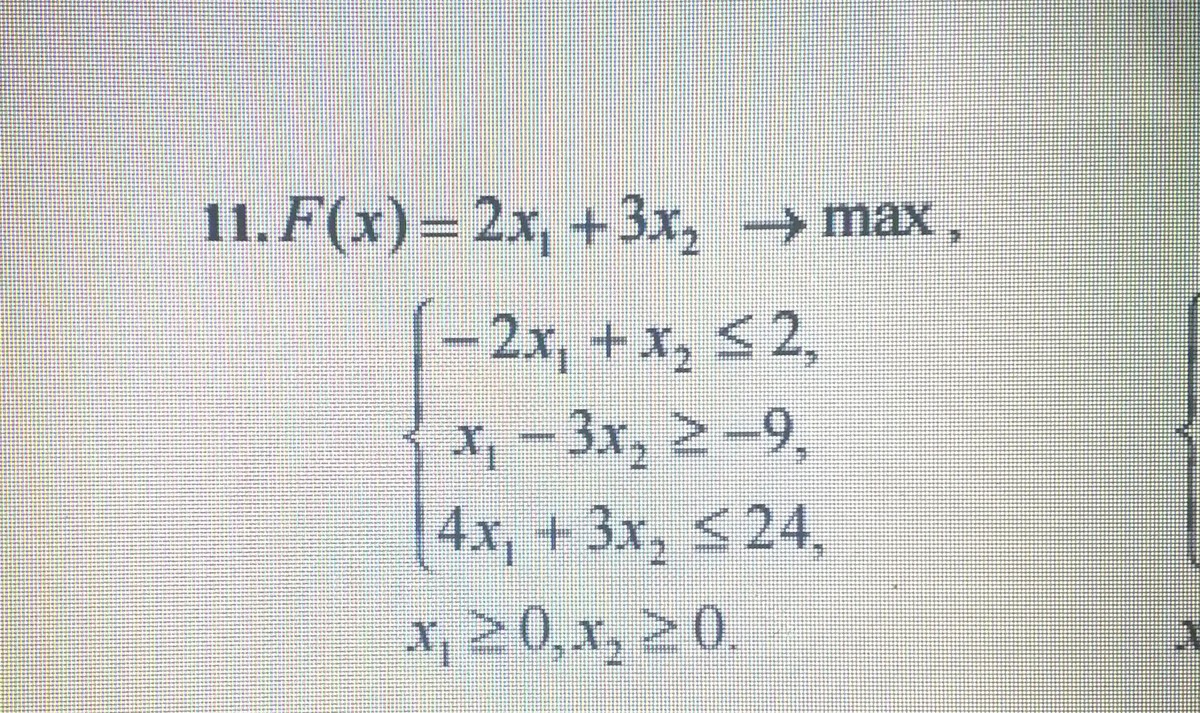


Ответы
Автор ответа:
0
Решение:
Приведём систему условий к каноническому виду:
Там, где стоит знак неравенства "<=", то к левой части добавляем еще одну новую переменную xi со знаком "+", а если знак неравенства ">=", то xi со знаком "-". xi >= 0).
Получаем систему уравнений:
-2*x1 + x2 + x3 = 2
-x1 + 3*x2 + x4 = 9
4*x1 + 3*x2 + x5 = 24
Находим базисные переменные:
Все переменные, которые входят один раз в систему уравнений и они с коэффициентом 1, называются базисными переменными. В нашем случае выберем следующие: x5, x3, x4
Составляем начальную таблицу:
* Вдоль каждой строки в таблице проставлены коэффициенты при неизвестных в уравнениях-условиях
* В первом столбце проставлены базисные переменные
* В последнем столбце свободные члены
* В последней строке стоят коэффициенты при неизвестных из функции F с обратным знаком
Применяем симплекс метод:
* Стремимся, чтобы в последней строке остались только положительные элементы или равные нулю
* Стремимся, чтобы в столбце свободных членов остались только положительные элементы
Для этого будем:
* Находить наибольшее значение по модулю в последней строке, Соответствующий элемент будет задавать ведущий столбец
* Находим минимальное отрицательное отношение элементов свободного столбца к элементам ведущего столбца, находим соответствующую ведущую строку
* На пересечении ведущей строки и ведущего столбца находится ведущий элемент
* Для всех строк кроме ведущей делаем преобразование: [новая строка] = [старая строка] - E[il] / E[ll] * [ведущая строка], где E[il] - элемент при пересечение ведущего столбца и текущей строки E[ll] - ведущий элемент
* Элементы ведущей строки делим на ведущий элемент
* На место базисного элемента в ведущей строке ставим переменную из ведущего столбца
1 шаг. Базисные переменные x5, x3, x4
Базисное решение x1 = 0, x2 = 0, x3 = 24, x4 = 9, x5 = 2
2 шаг. Базисные переменные x3, x4, x2
Базисное решение x1 = 0, x2 = 2, x3 = 18, x4 = 3, x5 = 0
3 шаг. Базисные переменные x3, x1, x2
Базисное решение x1 = 3/5, x2 = 16/5, x3 = 12, x4 = 0, x5 = 0
4 шаг
В последней строке остались только положительные элементы или равные нулю, в столбце свободных членов остались только положительные элементы, значит:
Оптимальное решение x1 = 3, x2 = 4, x3 = 4, x4 = 0, x5 = 0 Максимальное значение F = 2*x1 + 3*x2
Подставляем оптимальное решение, получим:
Fmax=2*3+3*4 = 18
Приведём систему условий к каноническому виду:
Там, где стоит знак неравенства "<=", то к левой части добавляем еще одну новую переменную xi со знаком "+", а если знак неравенства ">=", то xi со знаком "-". xi >= 0).
Получаем систему уравнений:
-2*x1 + x2 + x3 = 2
-x1 + 3*x2 + x4 = 9
4*x1 + 3*x2 + x5 = 24
Находим базисные переменные:
Все переменные, которые входят один раз в систему уравнений и они с коэффициентом 1, называются базисными переменными. В нашем случае выберем следующие: x5, x3, x4
Составляем начальную таблицу:
* Вдоль каждой строки в таблице проставлены коэффициенты при неизвестных в уравнениях-условиях
* В первом столбце проставлены базисные переменные
* В последнем столбце свободные члены
* В последней строке стоят коэффициенты при неизвестных из функции F с обратным знаком
Применяем симплекс метод:
* Стремимся, чтобы в последней строке остались только положительные элементы или равные нулю
* Стремимся, чтобы в столбце свободных членов остались только положительные элементы
Для этого будем:
* Находить наибольшее значение по модулю в последней строке, Соответствующий элемент будет задавать ведущий столбец
* Находим минимальное отрицательное отношение элементов свободного столбца к элементам ведущего столбца, находим соответствующую ведущую строку
* На пересечении ведущей строки и ведущего столбца находится ведущий элемент
* Для всех строк кроме ведущей делаем преобразование: [новая строка] = [старая строка] - E[il] / E[ll] * [ведущая строка], где E[il] - элемент при пересечение ведущего столбца и текущей строки E[ll] - ведущий элемент
* Элементы ведущей строки делим на ведущий элемент
* На место базисного элемента в ведущей строке ставим переменную из ведущего столбца
1 шаг. Базисные переменные x5, x3, x4
Базисное решение x1 = 0, x2 = 0, x3 = 24, x4 = 9, x5 = 2
2 шаг. Базисные переменные x3, x4, x2
Базисное решение x1 = 0, x2 = 2, x3 = 18, x4 = 3, x5 = 0
3 шаг. Базисные переменные x3, x1, x2
Базисное решение x1 = 3/5, x2 = 16/5, x3 = 12, x4 = 0, x5 = 0
4 шаг
В последней строке остались только положительные элементы или равные нулю, в столбце свободных членов остались только положительные элементы, значит:
Оптимальное решение x1 = 3, x2 = 4, x3 = 4, x4 = 0, x5 = 0 Максимальное значение F = 2*x1 + 3*x2
Подставляем оптимальное решение, получим:
Fmax=2*3+3*4 = 18
Похожие вопросы
Предмет: Английский язык,
автор: daraas
Предмет: Литература,
автор: pipukapipukachnaya
Предмет: Физика,
автор: Girl395
Предмет: Биология,
автор: Emma01