Question

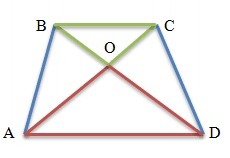
В трапеции ABCD с основаниями BC и AD диагонали пересекаются в точке О, BO=4 см, OD=20 см, AC=36 см. Найдите отрезки AO и OC.

Answer 1

Решим данную задачу на подобие треугольников.

1) $angle AOD=angle COB$ (как вертикальные)

2) $angle DAO=angle BCO$ (как внутренние накрест лежащие при $AD~||~BC$ и секущей $AC$)

Таким образом, треугольники AOD и COB подобны по двум углам.

Из подобия треугольников следует пропорциональность соответствующих сторон :

$displaystyle frac{AD}{BC}=frac{OD}{OB}=frac{AO}{OC}$

Зная, что AC = AO + OC откуда AO = AC - OC, имеем

$displaystyle frac{OD}{OB}=frac{AC-OC}{OC} ~~~Rightarrow~~~frac{OD}{OB}=frac{AC}{OC}-1\ \ frac{AC}{OC}=frac{OD}{OB}+1 ~~~Rightarrow~~~OC=frac{OBcdot AC}{OD+OB}=frac{4cdot36}{20+4} = 6$

Тогда AO = AC - OC = 36 - 6 = 30 см

Ответ: АО=30 см, ОС=6 см.