Предмет: Геометрия,
автор: КириллШу
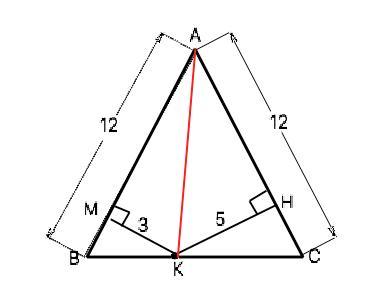
Точка К лежит на основании ВС равнобедренного треугольника АВС. Найдите площадь этого треугольника, если длины его боковых сторон АС и АВ равны 12,а расстояния от точки К до этих сторон равны соответственно 3и5. Заранее спасибо.
Ответы
Автор ответа:
0
Ответ: 48 (ед. площади)
Объяснение:
Расстояние от точки до прямой равно длине отрезка, проведенного перпендикулярно данной прямой.
Соединим вершину А и т.К. Отрезки КМ и КН - высоты ∆ АВК и ∆ АСК соответственно.
Площадь ∆ АВС равна сумме площадей треугольников АВК и АКС.
S(ABC)=S(ABK)+S(ACK)
S(АВК)=AB•KМ:2=12•3:2=18
S(АСК)=АС•КН:2-12•5:2=40 =>
S(ABC)=18+30=48 (ед. площади)
Приложения:
Похожие вопросы
Предмет: Оʻzbek tili,
автор: smul11
Предмет: Геометрия,
автор: dariab0909
Предмет: Английский язык,
автор: GNOMI4EK30003118EE
Предмет: Математика,
автор: karinaalieva