Предмет: Математика,
автор: lawandaa
Сторона основания правильной четырехугольной призмы равна корень из 2,а ее диагональ составляет с плоскостью боковой грани угол в 30 градусов. Найдите объем призмы.
Ответы
Автор ответа:
0
Ответ:
4 куб.см.
Пошаговое объяснение:
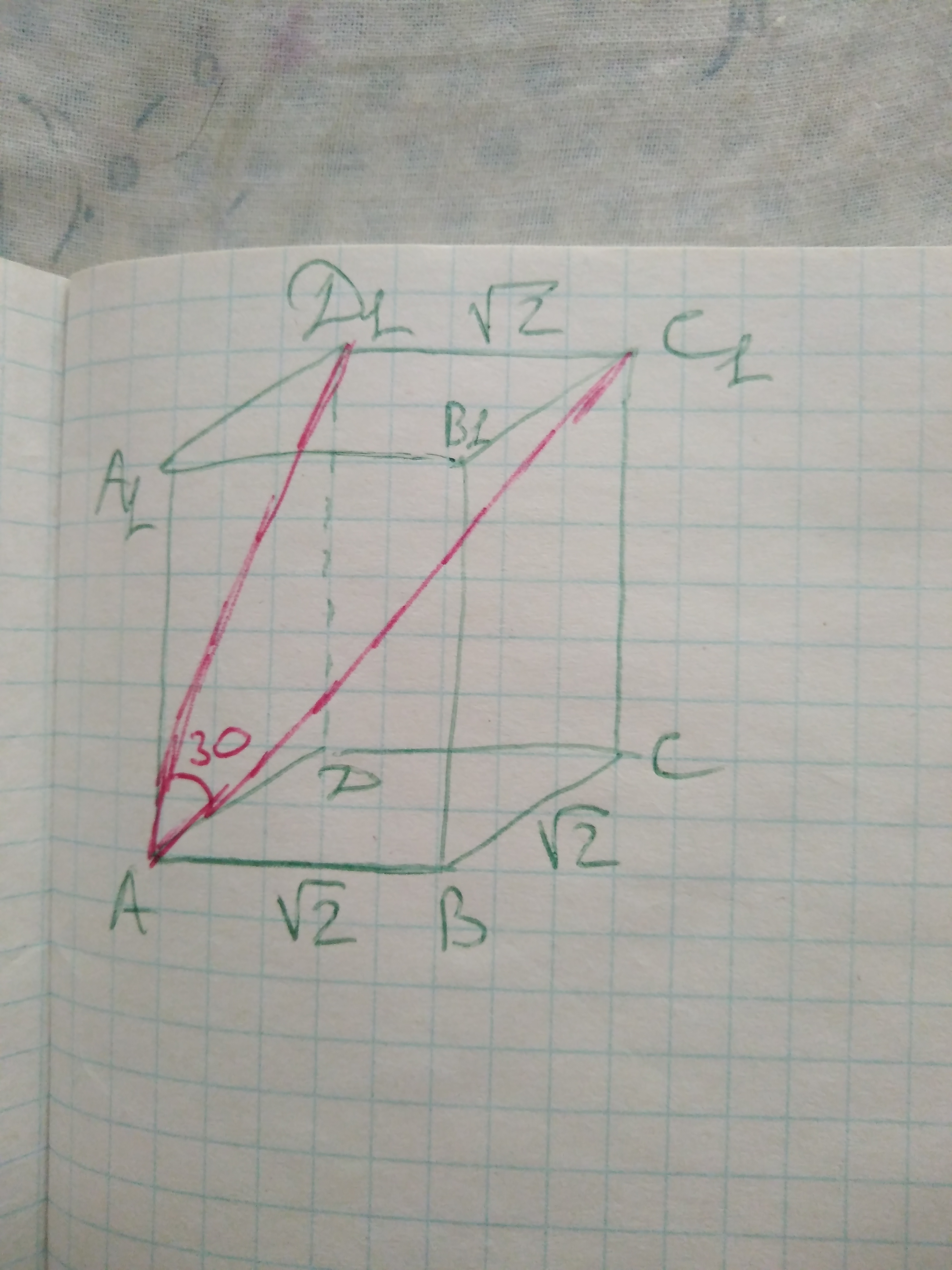
Вот рисунок. AB = BC = C1D1 = √2; AC = √2*√2 = 2
Угол между диагональю призмы AC1 и боковой плоскостью ADD1A1 - это на самом деле угол между диагональю призмы AC1 и диагональю грани AD1.
В треугольнике AC1D1 углы 90°, 30° и 60°.
Гипотенуза вдвое больше катета против угла 30 гр.
AC1 = 2*C1D1 = 2√2.
Теперь рассмотрим прямоугольный треугольник ACC1.
Высоту призмы CC1 найдем из теоремы Пифагора:
CC1^2 = AC1^2 - AC^2 = (2√2)^2 - 2^2 = 8 - 4 = 4
CC1 = √4 = 2
Объем призмы равен
V = AB*BC*CC1 = √2*√2*2 = 4 куб.см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: lyazzat001
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: tatisha17
Предмет: Химия,
автор: forvator