Предмет: Геометрия,
автор: ksyuta1102
Прямая, которая пересекает противоположные стороны параллелограмма, делит одну из них на отрезки 12 и 18 см, а площадь параллелограмма - в отношении 2:1. Найдите длину отрезков, на которые эта прямая делит другую сторону параллелограмма. Расмотритевсе возможные случаи.
Ответы
Автор ответа:
0
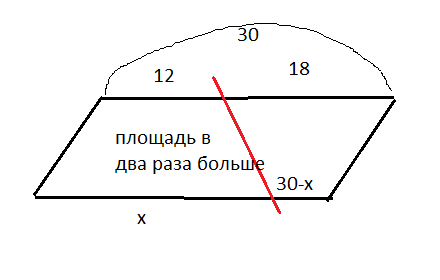
Прямая разбивает параллелограмм на две трапеции
(см. рисунок в приложении)
Основание, разделенное на части 12 и 18 в сумме дает 30
Значит и второе основание параллелограмма тоже 30.
Пусть оно разделено на части х и (30-х)
Найдем площадь трапеции с основаниями 12 и х и высотой h
S=(12+x)·h/2
Найдем площадь трапеции с основаниями 18 и (30-х) и высотой h
s=(18+(30-x))·h/2
По условию S ,больше s в два раза
(12+х)·h/2=2·(18+(30-x))·h/2
или
12+х=2·(18+30-х)
3х=84
х=28
Одна часть 28, вторая 30-28=2
Возможен второй случай
S меньше s в два раза
Тогда уравнение примет вид
2·((12+х)·h/2)=(18+(30-x))·h/2
24+2х=18+30-х
3х=24
х=8
30-х=30-8=22
Ответ 1) 28 см и 2 см
2) 8см и 22 см
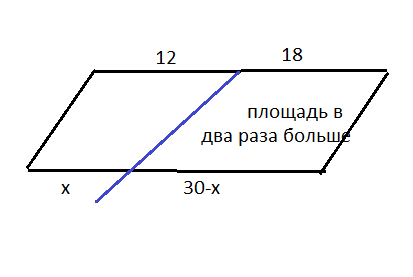
(см. рисунок в приложении)
Основание, разделенное на части 12 и 18 в сумме дает 30
Значит и второе основание параллелограмма тоже 30.
Пусть оно разделено на части х и (30-х)
Найдем площадь трапеции с основаниями 12 и х и высотой h
S=(12+x)·h/2
Найдем площадь трапеции с основаниями 18 и (30-х) и высотой h
s=(18+(30-x))·h/2
По условию S ,больше s в два раза
(12+х)·h/2=2·(18+(30-x))·h/2
или
12+х=2·(18+30-х)
3х=84
х=28
Одна часть 28, вторая 30-28=2
Возможен второй случай
S меньше s в два раза
Тогда уравнение примет вид
2·((12+х)·h/2)=(18+(30-x))·h/2
24+2х=18+30-х
3х=24
х=8
30-х=30-8=22
Ответ 1) 28 см и 2 см
2) 8см и 22 см
Приложения:
Похожие вопросы