Предмет: Геометрия,
автор: vinokurovbob
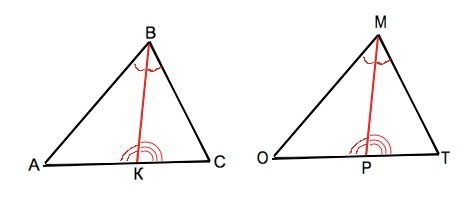
Докажите равенство двух треугольников по биссектрисе, углу, из вершины которого проведена эта биссектриса, и углу, образованному биссектрисой со стороной, к которой она принадлежит.
Ответы
Автор ответа:
0
В треугольниках АВС и ОМТ биссектрисы ВК и МР равны, угол АВК=углу ОМР, угол АКВ=углу ОРМ; угол КВС=РМТ.
а) ∆ АВЕ=∆ОМР по 2-му признаку равенства треугольников.
б) ∆ КВС= ∆РМТ по 2-му признаку равенства треугольников. ⇒
∆ АВС=∆ ОМТ, так как состоят из равных частей.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: valyaksa
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: rrttg
Предмет: Математика,
автор: romburkov