Предмет: Математика,
автор: Ivanova981
помогите решить пожалуйста
Приложения:
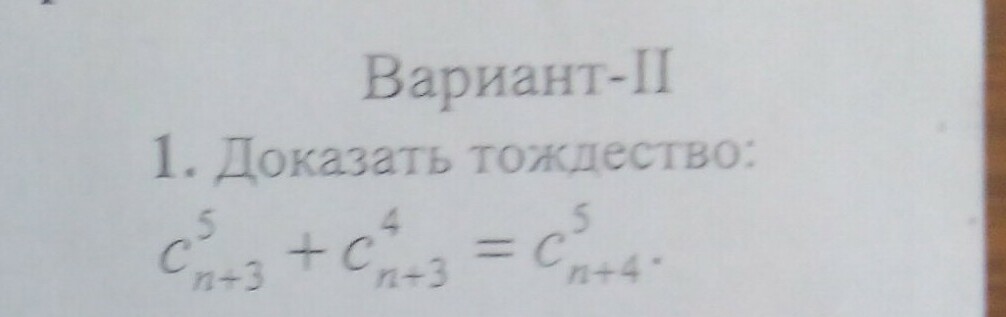
Ответы
Автор ответа:
0
Преобразуем левую часть равенства
преобразуем правую часть равенства
Сравним правую и левую части
Равенство доказано
Похожие вопросы
Предмет: Геометрия,
автор: mitrofanovairina75
Предмет: Русский язык,
автор: mnurkozha
Предмет: Английский язык,
автор: AELITAAJYLCIEVA
Предмет: Алгебра,
автор: alpine347
Предмет: История,
автор: nastyakiss21