Предмет: Геометрия,
автор: Bubllegum
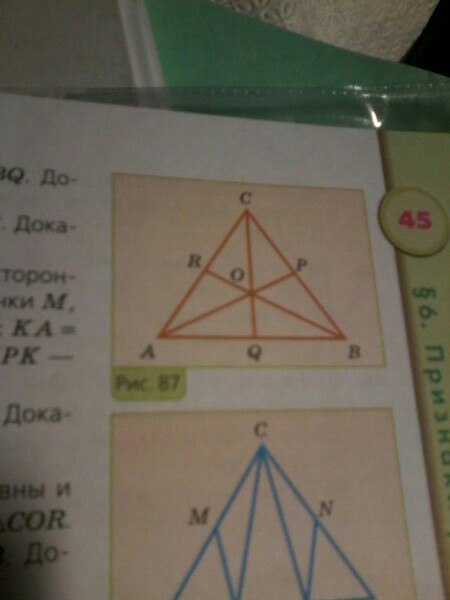
углы AOC и BOC на рисунке 87 равны. Докажите, что если OA=OB, то угол ABC= углу BAC и AQ=BQ Помогите, пожалуйста!!
Приложения:
Ответы
Автор ответа:
0
Думала, думала и надумала)
1. Рассмотрим ΔAOC и ΔBOC: ∠AOC=∠BOC (по условию), AO=OB (по условию), CO - общая сторона. ΔAOC=ΔBOC (по двум сторонам и углу между ними), следовательно, CB=CA.
2. Рассмотрим ΔCQA и ΔCQB: CQ - общая сторона, CB=CA (из равенства выше), ∠BCQ=∠ACQ (CQ - биссектриса ∠C). ΔCQA=ΔCQB (по двум сторонам и углу между ними), следовательно, AQ=BQ ,∠ABC=∠BAC / что и требовалось доказать.
1. Рассмотрим ΔAOC и ΔBOC: ∠AOC=∠BOC (по условию), AO=OB (по условию), CO - общая сторона. ΔAOC=ΔBOC (по двум сторонам и углу между ними), следовательно, CB=CA.
2. Рассмотрим ΔCQA и ΔCQB: CQ - общая сторона, CB=CA (из равенства выше), ∠BCQ=∠ACQ (CQ - биссектриса ∠C). ΔCQA=ΔCQB (по двум сторонам и углу между ними), следовательно, AQ=BQ ,∠ABC=∠BAC / что и требовалось доказать.
Автор ответа:
0
СПАСИБО ОГРОМНОЕ!!! НЕ ПРЕДСТАВЛЯЕШЬ КАК ПОМОГЛА <3
Автор ответа:
0
Всегда пожалуйста)
Похожие вопросы
Предмет: Математика,
автор: danilakantsur
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Геометрия,
автор: qwerx05
Предмет: Математика,
автор: asвапролд
Предмет: Математика,
автор: nick777kolya