Question

Помогите пожалуйста!Геометрия 11 класс
Нужно найти объем

Answer 1

1
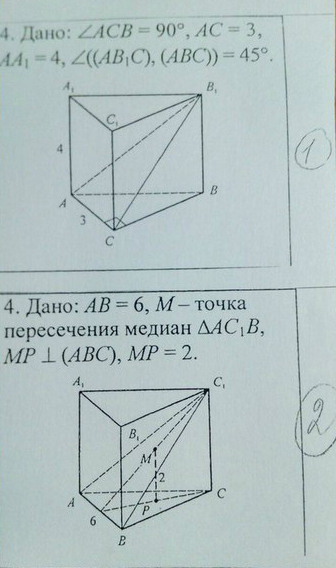
∠B₁CB - линейный угол двугранного угла между плоскостями (АВ₁С) и (АВС)
В₁С⊥ АС
ВС⊥АС
Δ ВВ₁С - равнобедренный прямоугольный, катет равны
ВС=ВВ₁=4   (АА₁=ВВ₁=СС₁=H)

V=S( основ)·Н=((1/2)·3·4)·4=24 куб. ед

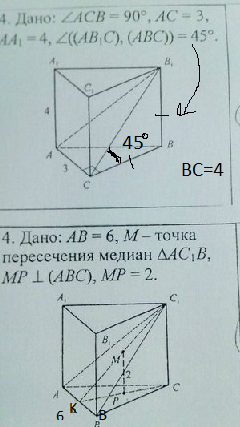
2.  Треугольник АВС - правильный ( другого быть не может, площадь треугольника по одной стороне не найти, если этот треугольник не является правильным)
S(правильного треуг)=а²√3/4

Медианы в точке пересечения делятся в отношении 2:1, считая от вершины, поэтому С₁M:MK=2:1 ,   а
KM:KC₁=1:3

Треугольники КМР и КСС₁ подобны
МР || СС₁
MP⊥ пл.(ABC)   и    СС₁⊥ пл.(АВС)

Из подобия
PM:CC₁=KM:KC₁=1:3

CC₁=3PM=6
Н=6 

V=S(осн)· Н=(6·√3/4)·6=9√3  куб. ед

Answer 2

Здесь картинка. Перед этим написано, что дано: прямая призма, правильный треугольник и т.д

Answer 3

Авторы заданий не обращают наэто внимания, копируют картинки, а условие неполное.

Answer 4

Задачи тестовые. Доказывать ничего не надо, надо дать ответ

Answer 5

Вы же видите скопированы 4-ые задачи. Но перенумерованы как 1 и2

Answer 6

Перед вариантом, состоящим из 4-х задач, написано то, чего нам не хватает, а школьникам все равно, что чего-то нет