Question

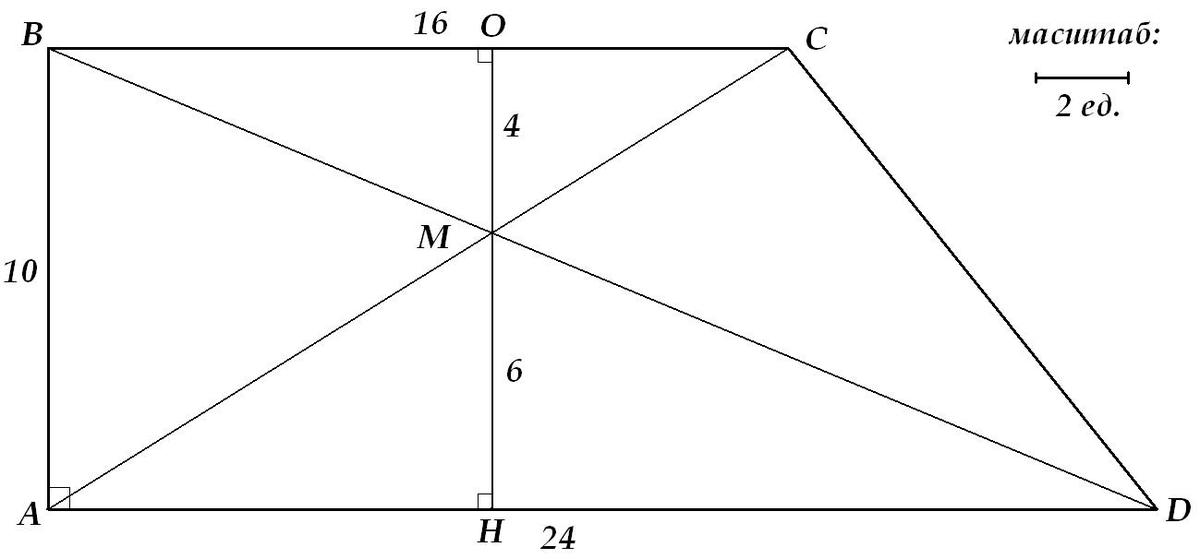
В прямоугольной трапеции АВСД (угол ВАД=90) с основаниями АД=24 и ВС=16 диагонали пересекаются в точке М, АВ=10. Найти площадь треугольника АМД.

Answer 1

Смотрим картинго (пропорци, между прочим, соблюдены):
Вспоминаем чудесное правило:
При пересесечении диагоналей трапеции, треугольники, лежащие на основаниях подобны. Доказывется это легко и самостоятельно, через равенство двух пар накрест лежащих и одной пары вертикальных углов.
ΔAMD~ΔCMB, MH и МО - высоты ΔAMD и ΔCMB, соответственно. Значит

$frac{AD}{BC}=frac{MH}{MO}$

Если кто-то готов с этим поспорить ну дерзните...

$frac{MH}{MO}=frac{24}{16}=frac{3}{2}\\MH=frac{AB}{3+2}cdot3=frac{10}{3+2}cdot3=6\\S_{AMD}= frac{ADcdotMH}{2}=frac{24cdot6}{2}=72$

Всё...

Answer 2

S(ABM)/S(AMD)  = BM/DM ,  но BM/DM = BC/DA  =16/24 =2/3  ||  ΔCMB ~ ΔAMD || ;
S(ABM)/S(AMD) =2/3 ;
S(ABM)/S(AMD) +1  =2/3+1 ;
S(ABD)/S(AMD) =5/3 ⇔S(AMD) =(3/5)*S(ABD) ⇒ 
S(AMD)=(3/5)*(24*10/2) =3*24*10/10 =72 (кв.ед.).

* * * ИЛИ по другому  Как  усложнять себе жизнь  * * *
Обозначаем S₁ =S(AMD); S₂ =S(CMB).  
S(ABCD) =(√S₁+√S₂)²  ;
(16+24)/2 * 10 =(√S₁+√S₂)² ;
200 = (√S₁+√S₂)² .
ΔAMD~ΔCMB ⇒S₂/S₁ =(BC/AD)² ; S₂/S₁ =(16/24)² ⇒√S₂ =(2/3)*√S₁.
-------
следовательно:
200 =((1+2/3)√S₁)²  ;
200 =(25/9)* S₁ ;
S₁ =200*9/25 =72 (кв.ед.) .