Question

Найдите наибольшее и наименьшее значение функции

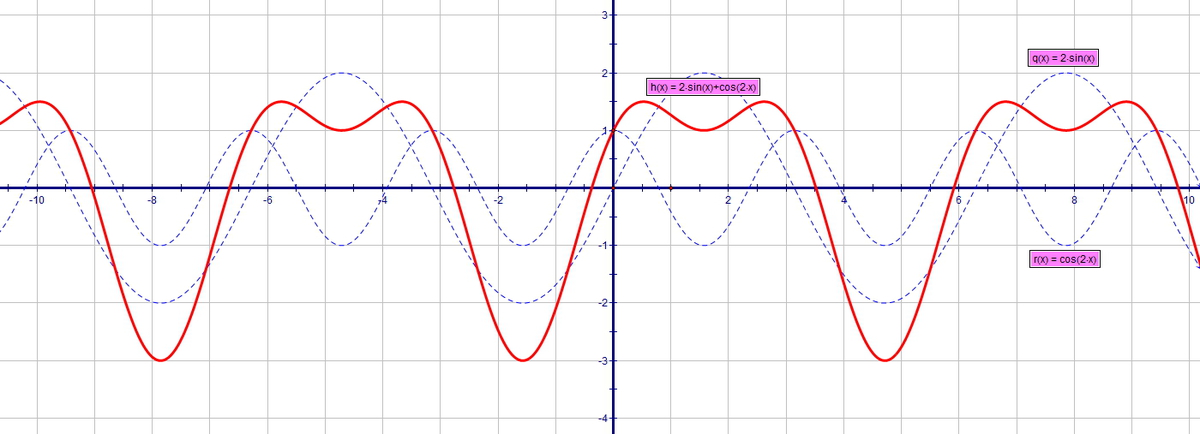
1) f(x)=2sinx+cos2x на отрезке [0; 2П]
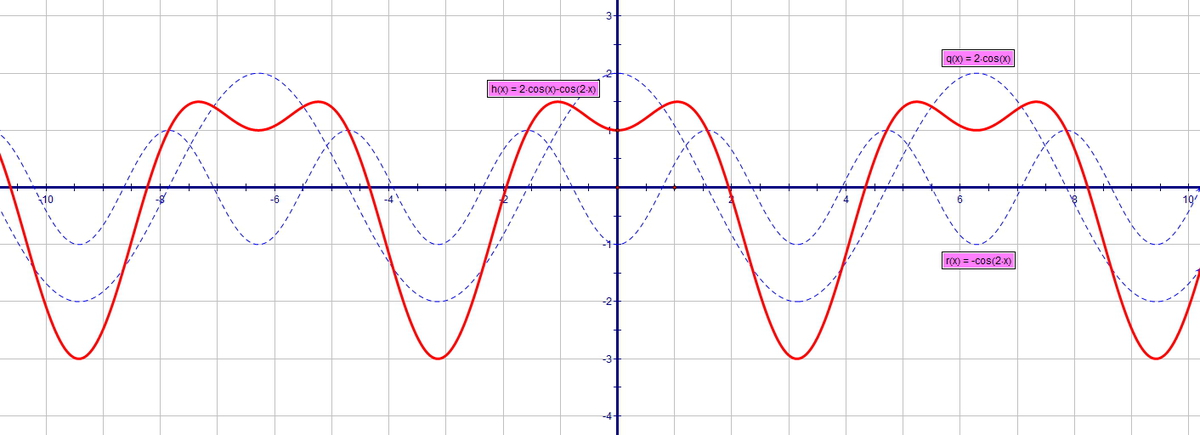
2) f(x)=2cosx-cos2x на отрезке [0; П]

Распишите все подробно, пожалуйста.

Answer 1

могу предложить графическое решение...
в обоих случаях
max 1.5
min  -3
1) f ' (x) = 2cosx - 2sin(2x) = 0
cosx - 2sinx*cosx = 0
cosx = 0 ---точка min --- для x = π/2   или   x = 3π/2 
sinx = 1/2 ---точка max --- для x = π/6   или  x = 5π/6
f(π/2) = 2*1 + (-1) = 1
f(3π/2) = 2*(-1) + (-1) = -3
f(π/6) = 1 + 1/2 = 1.5
f(5π/6) = 1 + 1/2 = 1.5
2) f ' (x) = -2sinx + 2sin(2x) = 0
2sinx*cosx - sinx = 0
sinx = 0 ---точка min --- для x = 0   или   x = π 
cosx = 1/2 ---точка max --- для x = π/3   на отрезке [0; π]
f(0) = 2*1 - 1 = 1
f(π) = 2*(-1) - 1 = -3
f(π/3) = 1 + 1/2 = 1.5

Answer 2

1) f(x) =2sinx +cos2x , x∈[π ;2π].
---
f(x) =2sinx +(1-2sin²x) = -2sin²x +2sinx +1 = -2(sinx - 1/2)² +1,5 .
maxf(x)=1,5 , если  sinx =1/2 .   x =π/6  или  π -π/6 =5π/6 .
minf(x) = -3 ,  если  sinx = -1.     x = 3π/2.
-------
2)  f(x) =2cosx -cos2x , x∈[0 ;π].
---
(x) =2cosx -(2cos²x -1) = -2cos²x +2cosx +1 = -2(cosx - 1/2)² +1,5 .
maxf(x)=1,5 , если  cosx =1/2 .   x =π/3  .
minf(x) = -3 ,  если  cosx = -1.     x = π.