Предмет: Геометрия,
автор: dasha17110
Стороны треугольника равны 3 и 6, угол между ними равен 60 градусов. Найти биссектрису треугольника, проведенную из вершины этого. угла.
Ответы
Автор ответа:
0
Смотрим картинго:
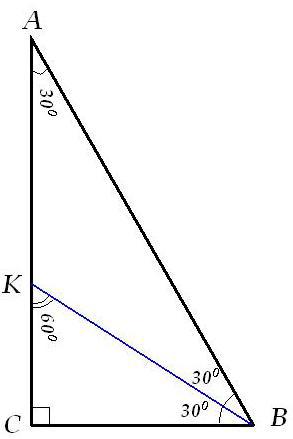
ΔАВС, АВ=6, ВС=3, ∠АВС=60°, ВК - биссектриса угла АВС
По теореме косинусов находим сторону АС. Ну так, на всякий случай, вдруг пригодится... ))

Что-то треугольник на картинке очень уж похож на прямоугольный...
Надо бы проверить...

Ну я же говорил прямоугольный; так и есть! ))
Смотрим на ΔВКС: все его углы равны углам ΔАВС, значит ΔВКС~ΔАВС/
Из пропорциональности прямоугольных треугольников находим биссектрису ВК:

ΔАВС, АВ=6, ВС=3, ∠АВС=60°, ВК - биссектриса угла АВС
По теореме косинусов находим сторону АС. Ну так, на всякий случай, вдруг пригодится... ))
Что-то треугольник на картинке очень уж похож на прямоугольный...
Надо бы проверить...
Ну я же говорил прямоугольный; так и есть! ))
Смотрим на ΔВКС: все его углы равны углам ΔАВС, значит ΔВКС~ΔАВС/
Из пропорциональности прямоугольных треугольников находим биссектрису ВК:
Приложения:
Автор ответа:
0
Спасибо большое
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: arbuz1725
Предмет: Русский язык,
автор: katagorna3
Предмет: Математика,
автор: fedorova2012
Предмет: Геометрия,
автор: Lovatic