Question

Боковые стороны равнобедренного треугольника равны 625, основание равно 350. Найдите радиус вписанной окружности.

Answer 1

Боковые стороны равнобедренного треугольника равны 625, основание равно 350. Найдите радиус вписанной окружности.

========================================================

Рассмотрим некоторые способы решения данной задачи:

▪Первый способ:

Применим общеизвестную формулу:  S = р • r

где S - площадь n-угольника , р = ( a₁ + а₂ +...+аₙ )/2 - полупериметр , r - радиус вписанной окружности в n-угольник.

p = ( AB + BC + AC )/2 = ( 625 + 625 + 350 )/2 = 800

Для нахождения площади ΔАВС пойдём двумя путями:

1) Найдём площадь по формуле Герона:

S = √( p•( p - a )•( p - b )•( p - c ) )

где р = ( а + b + c )/2 - полупериметр треугольника, а,b,c - стороны данного треугольника

S abc = √( ( 800•( 800 - 625 )•( 800 - 625 )•( 800 - 350 ) ) = √( 800•175•175•450 ) = 105 000

2)  ΔАВС - равнобедренный, ВН ⊥ АС ⇒ АН = НС = АС/2 = 350/2 = 175 - по свойству равнобедренного треугольника

Рассмотрим ΔАВН: по т. Пифагора

ВН² = АВ² - АН² = 6252 - 1752 = ( 625 - 175 )•( 625 + 175 ) = 450 • 800 = 360 000

ВН = 600

S abc = АС•ВН/2 = 350•600/2 = 105 000

r = S / p = 105 000 / 800 = 131,25

▪Второй способ:

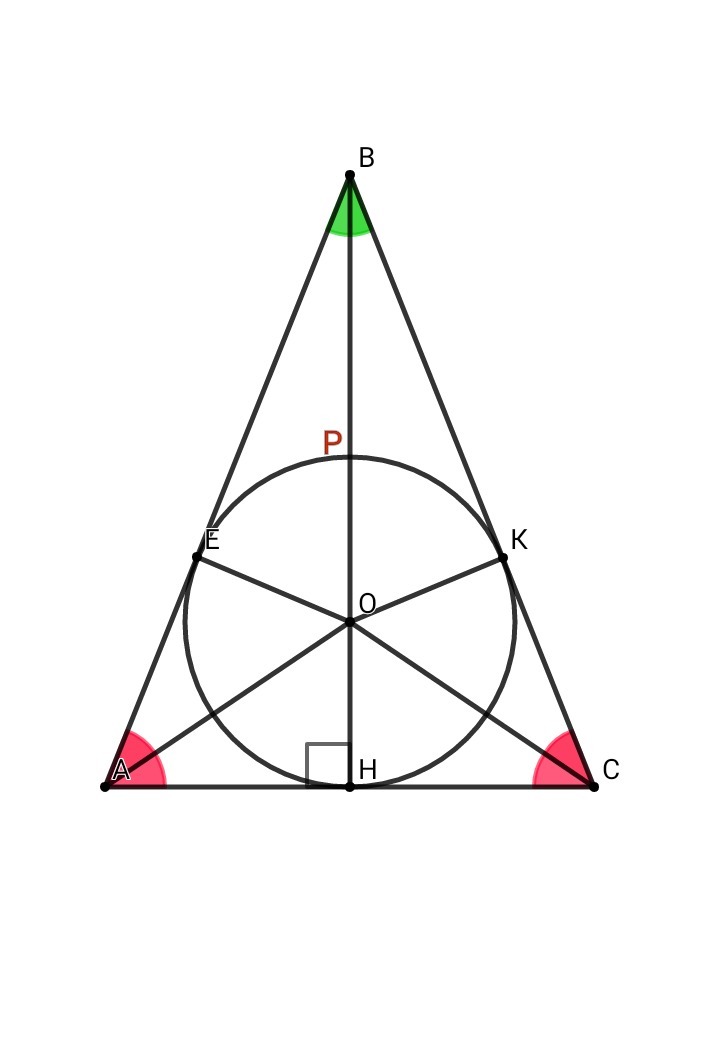
Точка О - центр вписанной окружности. Как известно, центром вписанной окружности является точка пересечения биссектрис ⇒ АО - биссектриса ∠А

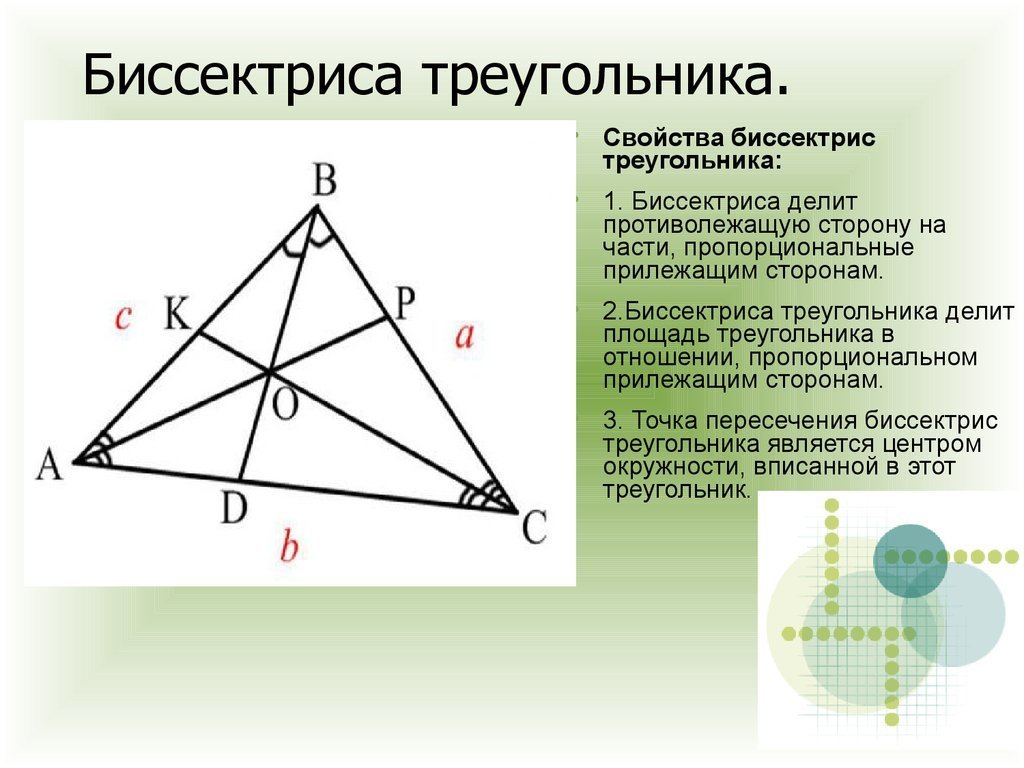
Применим свойство биссектрисы угла в тр. АВН ( см. приложение ):

Биссектриса угла в треугольнике делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам

ВО/ОН = АВ/АН = 625/175 = 25/7

Для нахождения ОН = r  пойдём двумя путями:

1) Пусть ОН = х, тогда ОВ = 600 - х

600 - х/х = 25/7

25х = 4200 - 7х

32х = 4200

х = 4200/32 = 131,25

2) Пусть ВО = 25х , ОН = 7х , тогда

ВО + ОН = ВН

25х + 7х = 600

32х = 600

х = 600/32 = 18,75

Отсюда  ОН = 7х = 7•18,75 = 131,25

▪Третий способ:

ΔВЕО подобен ΔВНА по двум углам:

∠ОВЕ - общий ; ∠ОЕВ = ∠АНВ = 90°

Составим отношения сходственных сторон:

ОВ/AB = BE/BH  ⇒  OB = AB•BE/BH = 625•450/600 = 468,75

OH = BH - OB = 600 - 468,75 = 131,25

▪Четвёртый способ:

Из теоремы об отрезках касательных, проведённых из одной точки, следует ( см. приложение ):

АН = АЕ = НС = СК = 175 ;  ВК = ВЕ = АВ - АЕ = 625 - 175 = 450

Из теоремы о касательной и секущей следует ( см. приложение ):

Пусть BP = x, тогда

ВЕ² = BP • BH

450² = х • 600

х = 450² / 600 = 337,5

ОН = РН / 2 = ВН - ВР / 2 = 600 - 337,5 / 2 = 262,5 / 2 = 131,25

▪Пятый способ:

cos∠A = AH/AB = 175/625 = 7/25

Данный прямоугольный треугольник АВН подобен прямоугольному треугольнику с катетами 24 и 7 и гипотенузой 25  ⇒  tg∠A = 24/7

Пусть ∠НАО = α , тогда ∠А = 2α

Используем тригонометрическую формулу:

tg2α = 2tgα/ ( 1 - tg²α )

24/7 = 2tgα / ( 1 - tg²α )

24 - 24tg²α = 14tgα

12tg²α + 7tgα - 12 = 0

Пусть tgα = t , тогда

12t²+ 7t - 12 = 0

D = 7² - 4•12•(-12) = 49 + 576 = 625 = 25²

t₁ = ( - 7 - 25 )/24 = - 32/24 = - 4/3 - не подходит, так как ∠А - острый

t₂ = ( - 7 + 25 )/24 = 18/24 = 3/4

Отсюда  tga = 3/4

Рассмотрим ΔАОН:

tgα = OH/AH = 3/4

OH = AH • 3 / 4 = 175 • 3 / 4 = 525/4 = 131,25

ОТВЕТ: 131,25