Question

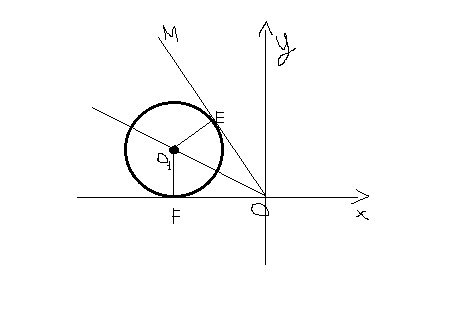
На рисунке окружность касается оси Ox в точке F, а луча OM -в точке E;Угол F01E=120 градусов, OO1=2 корня из 3. Напишите уравнение этой окружности. Щас рисунок скину, погодите. И поясните, как делали, пожалуйста

Answer 1

B  ΔOO1F  ∠O1OF=90-120/2=30 Тогда О1F=2√3/2=√3   R=√3
найдем координаты центра окружности
ордината у=√3
абсцисса х=ОF
OF=√OO1^2-O1F^2=√(2√3)^2-√3^2=√12-3=√9=3 Имеем
(x-3)^2+(y-√3)^2=√3^2
(x-3)^2+(y-√3)^2=3 ур-е окружности