Question

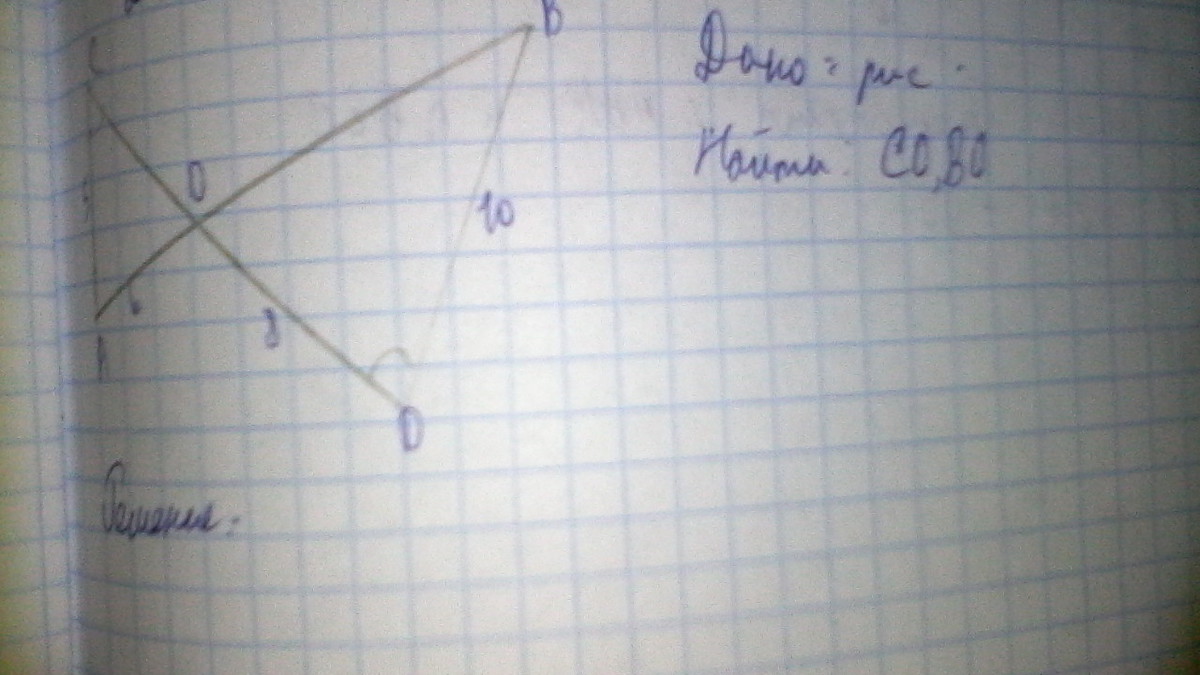
AC=5,AO=6,DB=10,OD=8
Найти:СO,BO

Answer 1

Треугольник АОС подобен треугольнику СОD  по двум углам
∠АСО=∠BDO  по условию
∠COA=∠BOD   как вертикальные
Из подобия треугольников следует пропорциональность сторон
АС:BD=CO:OD    ⇒   5:10=CO:8    ⇒  10CO=5·8  ⇒     CO=4
АС:BD=AO:OB    ⇒   5:10=6:OB    ⇒  5·OB=10·6   ⇒   OB=12

Answer 2

Это вертикальные углы поэтому углы у них равны.
Отрезки CO и AO соединяет отрезок CA 5см , а 
отрезки OD и BD соединяет отртезок BD 10 см .
Если через точку O провести прямую то BD будет в параллельной плоскости от CA отсюда и делаем вывод что если BD в 2 раза больше (BD:CA) то и все отрезки в его полуплоскости ( OD и BD ) будут в 2 раза больше параллельных им отрезкам из другой полуплоскости ( CO и AO ).
Вычисление:
BD:CA=2 (разница)
CO параллельна OD значит OD:2=8:2=4 см CO , а
BO параллельна AO значит AO*2=6*2=12 см BO 
(умножаем потому что в другой полуплоскости (там отрезки в 2 раза меньше чем в полуплоскости где находиться BD )

Answer 3

сделай ответ лучшим