Question

Помогите плиз решить
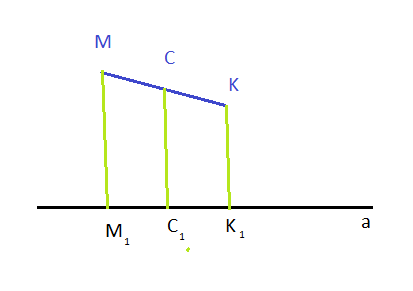
1)Отрезок MK не пересекает прямую а . Из его концов и середины С
проведены перпендикуляры MM1,KK1,CC1 к прямой а . Найдите СС1,если
MM1=16, KK1=6
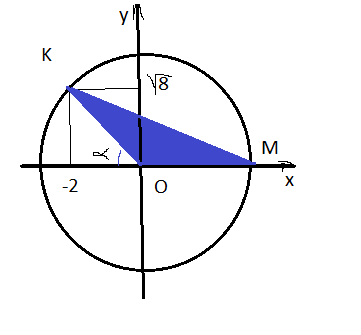
2)Окружность,заданная уравнением x^2 + y^2=12с, пересекает
положительную полуось Ox в точке М , точка K лежит на окружности , её
абцисса равна -2 . найдите площадь треугольника OKM

Answer 1

1) См. рисунок   ММ₁⊥ а;    СС₁ ⊥а;   КК₁⊥а   ⇒   ММ₁ || СС₁ || КК₁

ММ₁К₁К - трапеция
СС₁- средняя линия трапеции
СС₁=(ММ₁+КК₁)/2=(16+6)/2=11

2) Точка M имеет абсциссу х=√(12) =2√3 ординату у=0
   Точка  К имеет асбциссу х=-2   ордината у находится из уравнения
у²=12-4
у=√8
у=2√2
точка O (0;0)
ОМ имеет длину 2√3
ОМ- радиус вектор
ОМ=2√3
ОМ=ОК=2√3

tg∠КОМ=-√2 ( так как тангенс смежного с ним угла α равен √2    tg α=2√2/2=√2)
cos²∠КОМ= 1/(1+tg²∠KOM)=1/3
sin²∠КОМ=1-cos²∠KOM=1-(1/3)=2/3
sin ∠KOM=√(2/3)
S=ОК·ОМ· sin ∠KOM/2= (2√3)²·(√(2/3))/2=2√6 кв. ед