Question

Умоляю! Помогите с обратными тригонометрическими функциями!((

Answer 1

1) ... = 3^3 = 27
2) --- = 3/4 = 0.75
3) =0
4) ... = 187/205
5) = pi - 4*(-pi / 2) = pi + 2pi = 3pi

Answer 2

Спасибо вам огромное!!! Вы бог!!!=)

Answer 3

нет, я человек... и иногда ошибаюсь)) надеюсь, не в этот раз...

Answer 4

хах) все мы ошибаемся) спасибо еще раз огромное!

Answer 5

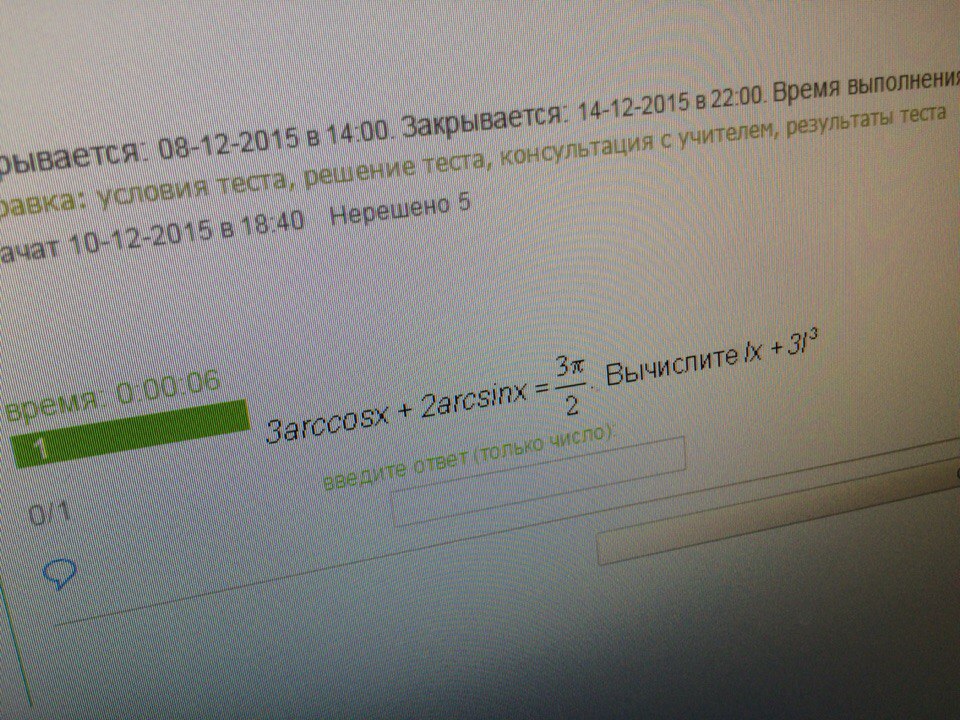
3arccosx +2arcsinx =3π/2⇔3(arccosx +arcsinx) - arcsinx = 3π/2⇔ 3π/2 - arcsinx = 3π/2
⇒x =0,  следовательно  (x+3)³ =(0+3)³ =27.
---
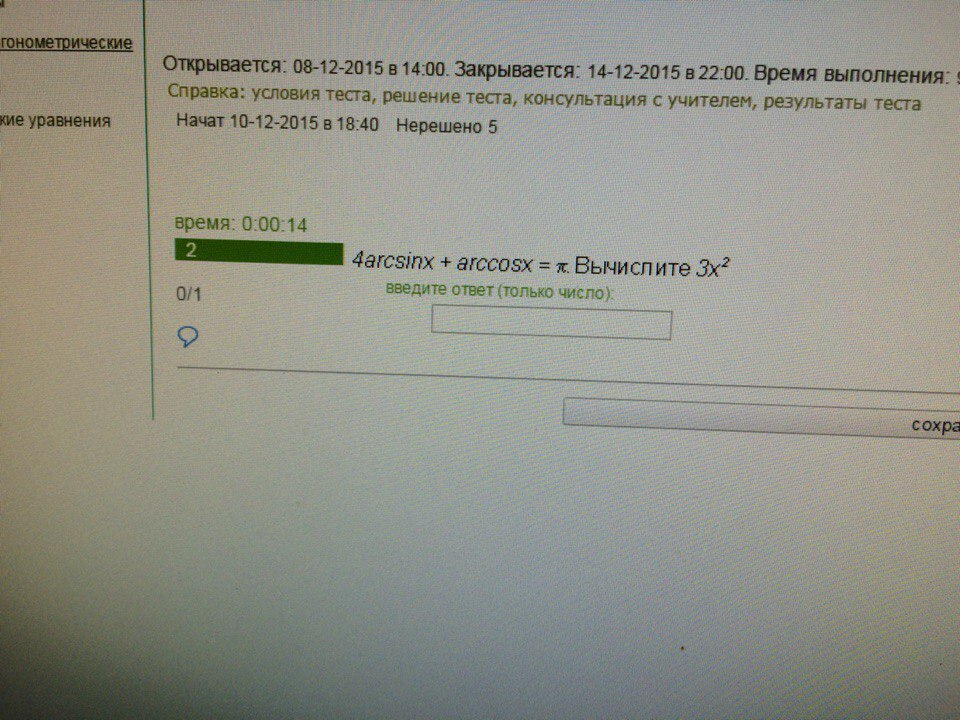
4arcsinx +arccosx =π ⇔3arcsinx+ (arcsinx +arccosx) =π ⇔3arcsinx +π/2 =π⇔
arcsinx =π/6 ⇒ x =1/2 ,следовательно  3x² =3*(1/2)²  =3/4. 
---
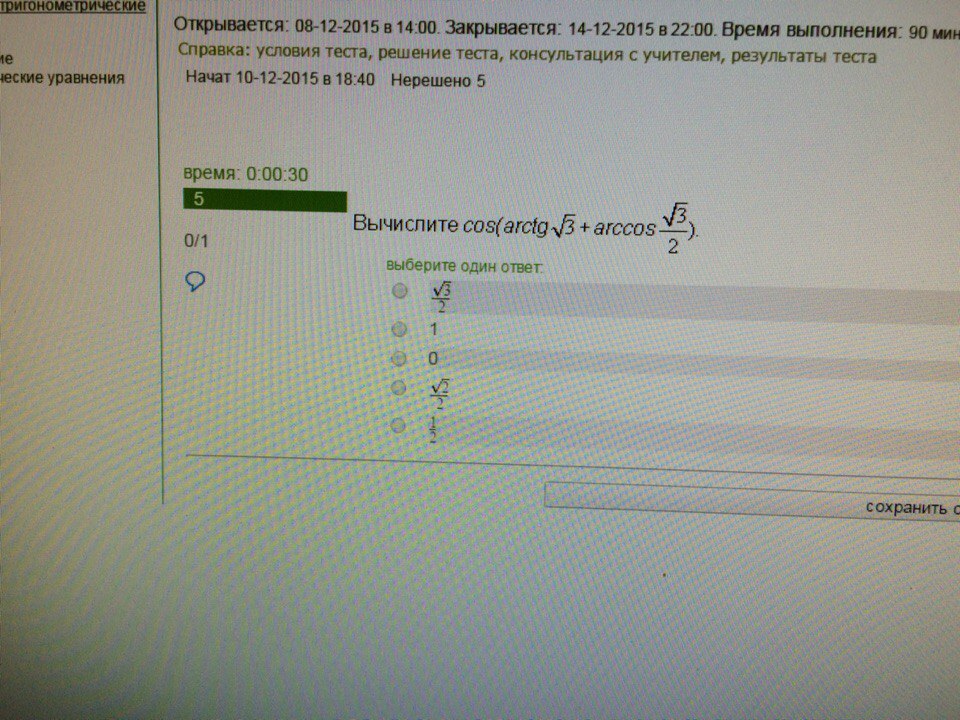
cos(arctq√3 +arccos√3/2) = cos(π/3 +π/6)  =  cosπ/2 =0.
---
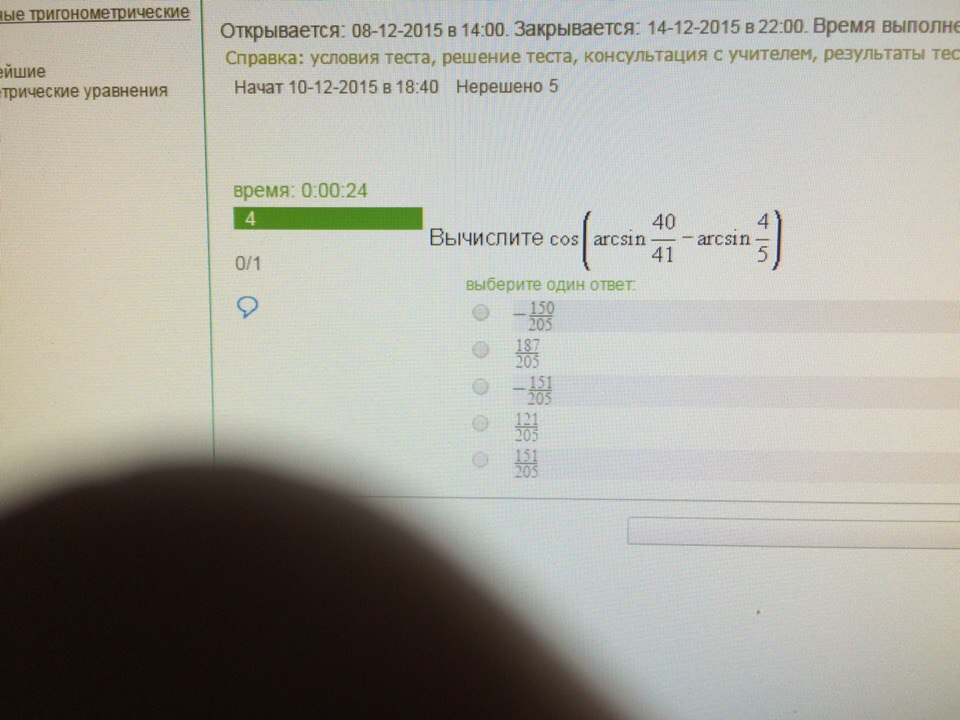
cos(arcsin40/41 -arcsin4/5) =cos(arcsin40/41)*cos(arcsin4/5) +sin(arcsin40/41)*sin(arcsin4/5) =cos(arccos9/41)*cos(arccos3/5) +40/41*4/5 =
9/41*3/5) +40/41*4/5 =(27+160)/5*41 = 187/205.

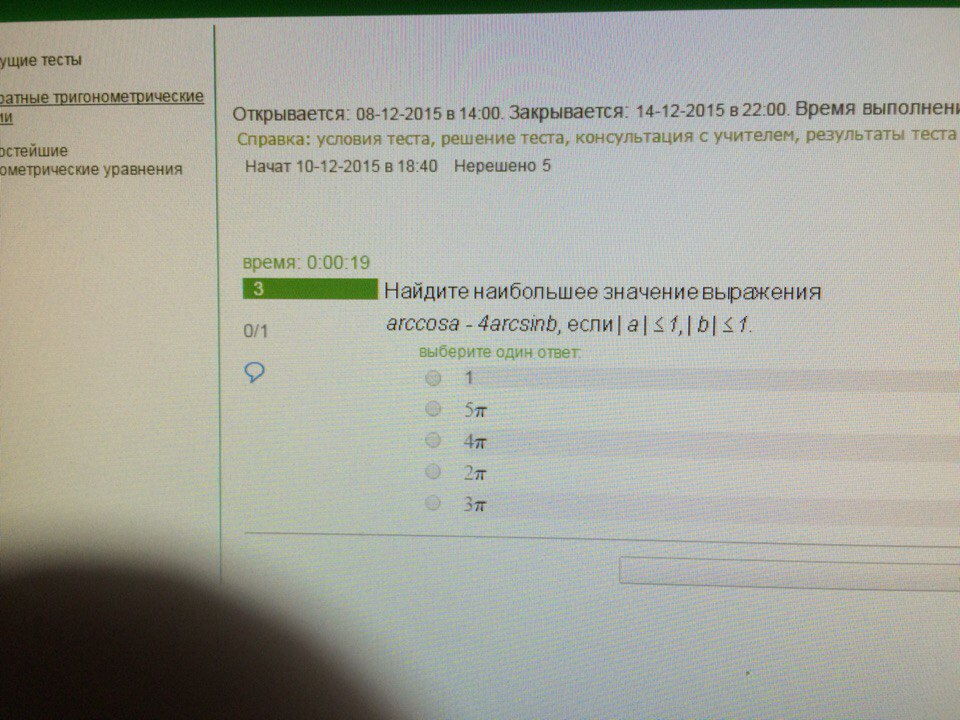
|a| ≤1 ,|b| ≤1 .
max(arccosa -4arccosb)  = π -4(-π/2) = π +2π =3π.