Предмет: Алгебра,
автор: Akula17
ПОМОГИТЕ С ДОМАШНИМ ЗАДАНИЕМ ПО АЛГЕБРЕ .
РАСПИШИТЕ ПОДРОБНО С ОБЪЯСНЕНИЯМИ .
Приложения:
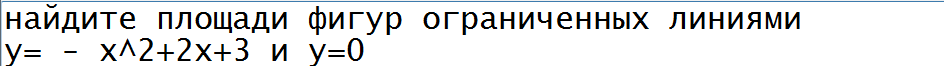
Ответы
Автор ответа:
0
Парабола  имеет ветви, направленные вниз, т.к. коэффициент перед х² отрицателен. Вершина в точке (1,4), точки пересечения с осью ОХ: (-1,0) и (3,0). Прямая у=0 -это ось ОХ. Имеем область между линией параболы и осью ОХ.
имеет ветви, направленные вниз, т.к. коэффициент перед х² отрицателен. Вершина в точке (1,4), точки пересечения с осью ОХ: (-1,0) и (3,0). Прямая у=0 -это ось ОХ. Имеем область между линией параболы и осью ОХ.

Приложения:

Автор ответа:
0
а как график будет выглядеть в этом задании , можете вложить его ??
Автор ответа:
0
Через указанные точки провести параболу не трудно
Автор ответа:
0
можете начертить его ?
Автор ответа:
0
Найдем границы интегрирования
-x²+2x+3=0
x²-2x-3=0
x1+x2=2 U x1*x2=-3
x1=-1 U x2=3
Так как ветви параболы у=-х²+2х+3 направлены вниз,то фигура ограничена сверху графиком параболы,а снизу осью ох
Площадь равна интегралу от -1 до 3 функции у=-х²+2х+3.Найдем производную и подставим пределы интегрирования
S=-x³/3+x²+3x|3-(-1)=-27/3+9+9-1/3-1+3=111-1/3=10 2/3
-x²+2x+3=0
x²-2x-3=0
x1+x2=2 U x1*x2=-3
x1=-1 U x2=3
Так как ветви параболы у=-х²+2х+3 направлены вниз,то фигура ограничена сверху графиком параболы,а снизу осью ох
Площадь равна интегралу от -1 до 3 функции у=-х²+2х+3.Найдем производную и подставим пределы интегрирования
S=-x³/3+x²+3x|3-(-1)=-27/3+9+9-1/3-1+3=111-1/3=10 2/3
Приложения:

Похожие вопросы
Предмет: Литература,
автор: diyaaaa49
Предмет: Қазақ тiлi,
автор: toleubainazerke0924
Предмет: Физика,
автор: dtugut
Предмет: Информатика,
автор: PoLiNkAmAlInKa200