Предмет: Геометрия,
автор: K1LLeReZGame
В окружности радиус которой равен 25 см проведены 2 параллельные хорды. Длины которых 40 и 30см. Найдите расстояние между ними.
Ответы
Автор ответа:
0
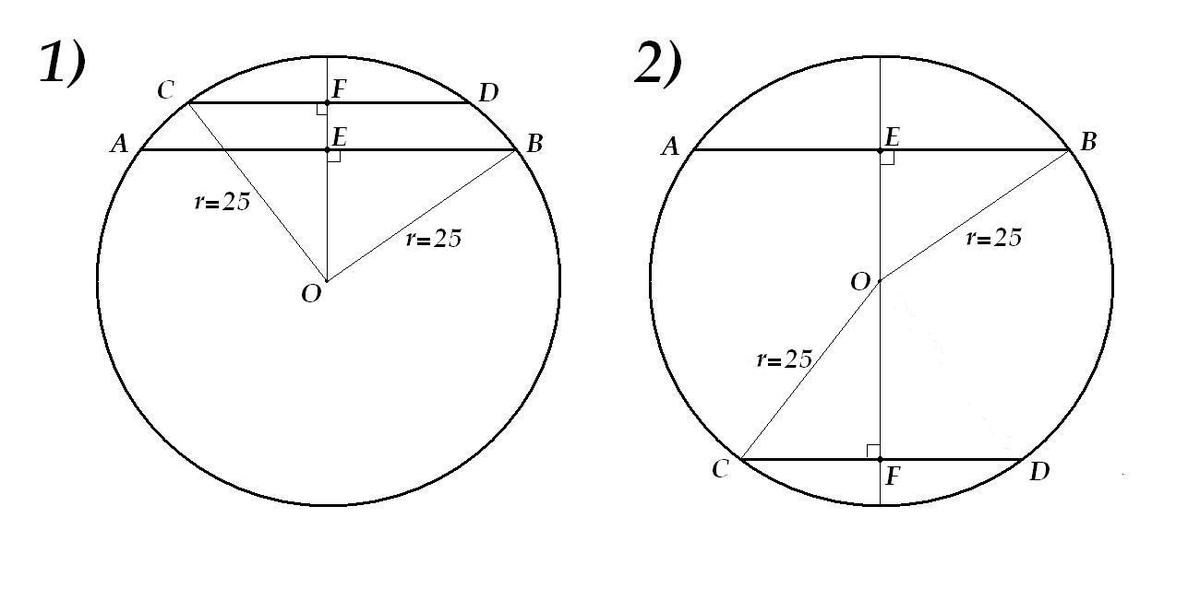
Смотрим картинго, и вспоминаем одно из свойств хорды:
Радиус, перпендикулярный хорде, делит эту хорду пополам.
Значит:
 cм
cм
 cм
cм
 см
см
 см
см
Искомое расстояние между хордами:
 см
см
Задача имеет второе решение, в случае, если хорды лежат по разные стороны от диаметра, параллельного им обеим (картинго №2).
Все обозначения верны для предыдущих вычислений, в этом случае:
 см
см
Радиус, перпендикулярный хорде, делит эту хорду пополам.
Значит:
Искомое расстояние между хордами:
Задача имеет второе решение, в случае, если хорды лежат по разные стороны от диаметра, параллельного им обеим (картинго №2).
Все обозначения верны для предыдущих вычислений, в этом случае:
Приложения:
Похожие вопросы
Предмет: Химия,
автор: deleted-20187992
Предмет: Английский язык,
автор: ekaterinabutkevich20
Предмет: Математика,
автор: barylkomatvij
Предмет: Математика,
автор: цуценя