Question

Одна из двух равных окружностей проходит через центр другой окружности.

Вычисли длину общей хорды, если радиус окружности равен 8 м.

Answer 1

Вполне логично, что если одна из двух равных окружностей проходит через центр второй окружности, то и вторая окружность проходит через центр первой.
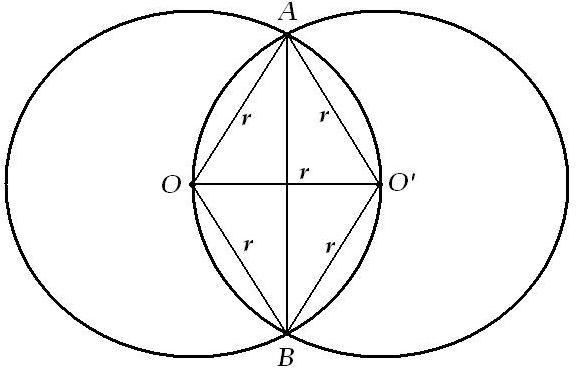
Смотрим рисунок:
Видим ромб $AO'BO$, со стороной и малой диагональю равными $r=8$ см. АВ - общая хорда.
Далее всё по т. Пифагора:
$AB=2sqrt{r^2-(frac{r}{2})^2}=2sqrt{8^2-4^2}=2sqrt{64-16}=2 sqrt{48}=8sqrt{3}$ см