Предмет: Алгебра,
автор: SSaSS
Решите пожалуйста, очень надо.
Приложения:
Ответы
Автор ответа:
0
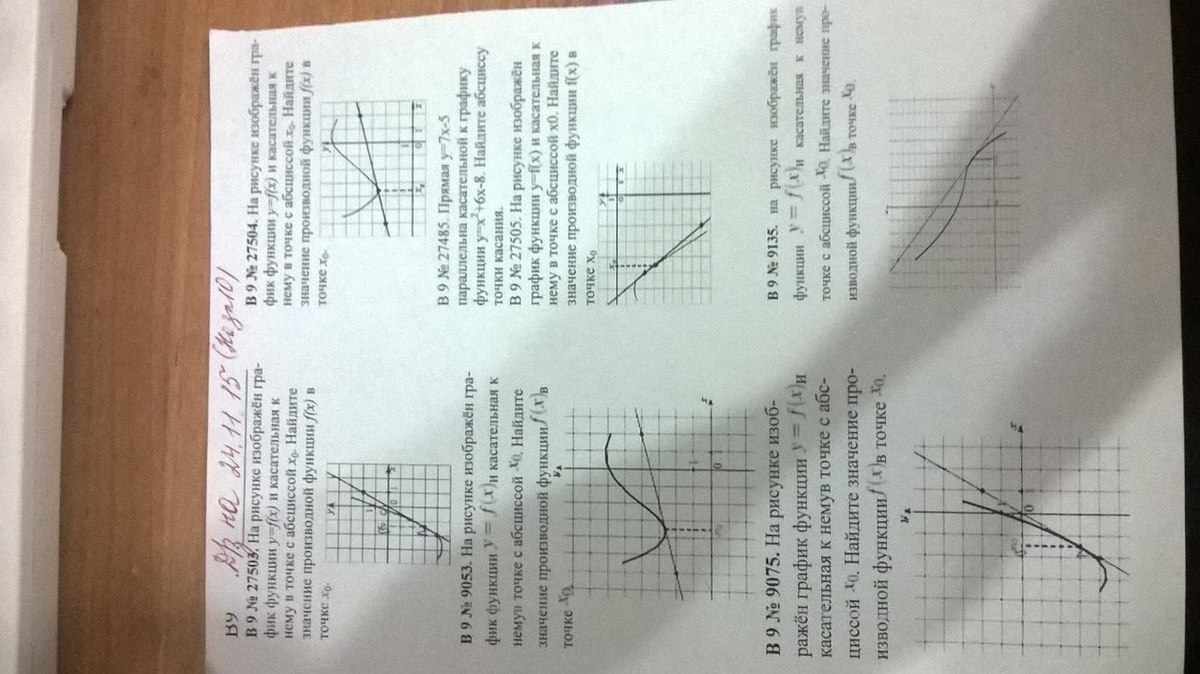
27503 Значение производной в точке касания равно угловому коэффициенту касательной, а это есть тангенс угла наклона касательной :

27504 Значение производной в точке касания равно угловому коэффициенту касательной, а это есть тангенс угла наклона касательной :

9053

9075

27505

27485 Значение производной в точке касания равно угловому коэффициенту касательной. Т.к. касательная параллельна прямой y = 7x - 5 то их угловые коэффициенты равны, и абсцисса точки касания находится из уравнения:

Ответ: 0,5
27504 Значение производной в точке касания равно угловому коэффициенту касательной, а это есть тангенс угла наклона касательной :
9053
9075
27505
27485 Значение производной в точке касания равно угловому коэффициенту касательной. Т.к. касательная параллельна прямой y = 7x - 5 то их угловые коэффициенты равны, и абсцисса точки касания находится из уравнения:
Ответ: 0,5
Похожие вопросы
Предмет: Английский язык,
автор: hop688
Предмет: Математика,
автор: daniellaabdrahmanova
Предмет: Биология,
автор: eugenemikh000
Предмет: Математика,
автор: romanovaoksana