Предмет: Алгебра,
автор: Эля0202
Помогите решить,завтра кр
Приложения:
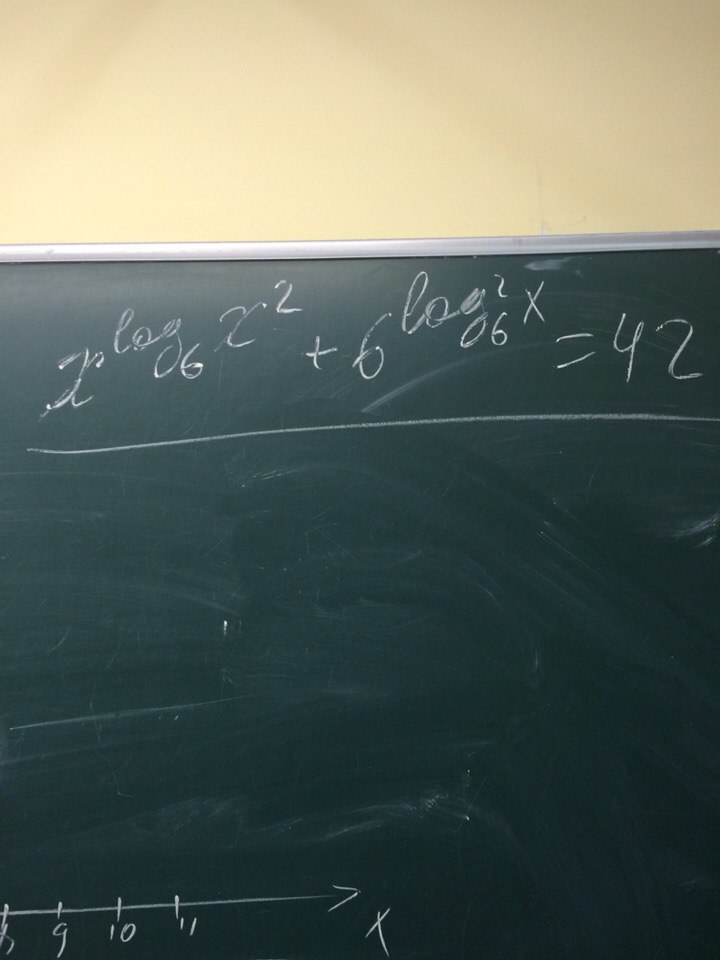
Ответы
Автор ответа:
0
Уравнение не имеет решений, т.к. аргумент у логарифма должен быть положительным.
Ответ:
Похожие вопросы
Предмет: Химия,
автор: nikolaenkovlad93
Предмет: Алгебра,
автор: 2829rz1983
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: fed09
Предмет: Геометрия,
автор: OLEGATOR228