Предмет: Геометрия,
автор: timosha2202344
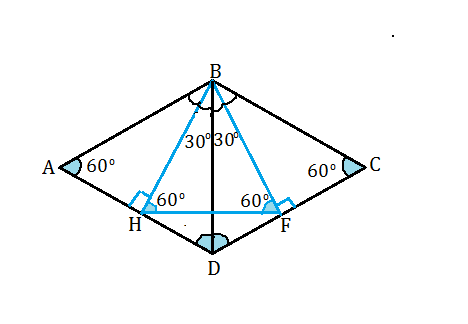
В ромбе ABCD угол A=60 градусов, BH,BF-высоты. Вычислите площадь ромба, если периметр HBF-равен 12 см
Ответы
Автор ответа:
0
Проведем диагональ ВD.
Треугольник АВD - равнобедренный с углом при А=60°
Отсюда углы при ВD =(180°-60°):2=60°
Треугольник АВD=∆ ВСD- равносторонние.
ВН - высота. ВН=ВF
∆ НВF - равнобедренный.
Угол НВF=60°
Углы при НF= по 60°
∆ НВF - равносторонний
ВН=ВФ= Р∆ ВНF:3=12:3=4 см
Высота равностороннего треугольника равна стороне, умноженной на синус 60°
ВН=АВ*(√3):2 см
АВ=ВН:(√3):2)=8:√3 см
Площадь параллелограмма ( а ромб - параллелограмм) равна произведению его смежных сторон, умноженному на синус угла между ними
Ѕ♢= (8:√3)*(√3):2=4 см²
-------
Сторону ромба можно найти по т.Пифагора:
АВ=√(ВН²+АН²), где АН=АВ:2.
Площадь равна произведению высоты на сторону. -
Проверьте - получите то же значение стороны и площади ромба.
Треугольник АВD - равнобедренный с углом при А=60°
Отсюда углы при ВD =(180°-60°):2=60°
Треугольник АВD=∆ ВСD- равносторонние.
ВН - высота. ВН=ВF
∆ НВF - равнобедренный.
Угол НВF=60°
Углы при НF= по 60°
∆ НВF - равносторонний
ВН=ВФ= Р∆ ВНF:3=12:3=4 см
Высота равностороннего треугольника равна стороне, умноженной на синус 60°
ВН=АВ*(√3):2 см
АВ=ВН:(√3):2)=8:√3 см
Площадь параллелограмма ( а ромб - параллелограмм) равна произведению его смежных сторон, умноженному на синус угла между ними
Ѕ♢= (8:√3)*(√3):2=4 см²
-------
Сторону ромба можно найти по т.Пифагора:
АВ=√(ВН²+АН²), где АН=АВ:2.
Площадь равна произведению высоты на сторону. -
Проверьте - получите то же значение стороны и площади ромба.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: fortniteepicgames240
Предмет: Биология,
автор: annvv
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: MisterHollms
Предмет: Биология,
автор: Юлия895