Предмет: Алгебра,
автор: Аноним
Очень срочно нужно )))
Приложения:
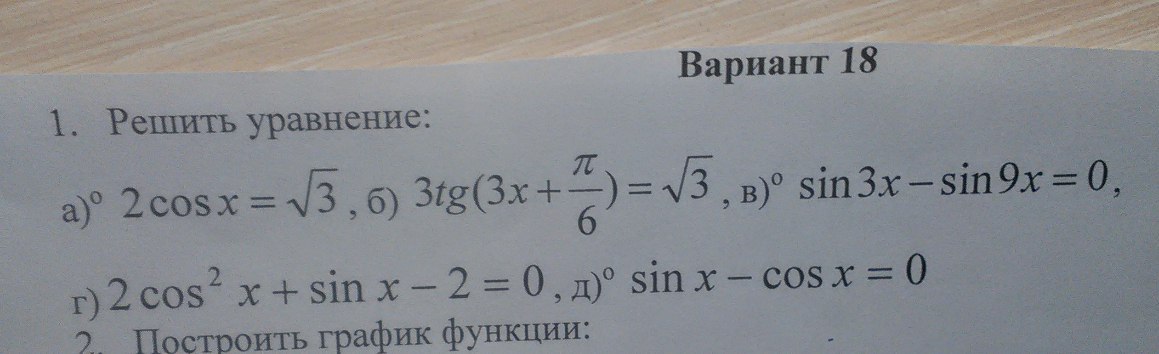
Ответы
Автор ответа:
0
1.  k - целое число.
k - целое число.
2. k _целое число.
k _целое число.
3. k и n - целые числа.
k и n - целые числа.
4. k и n - целые числа.
k и n - целые числа.
5. Предположим, что cosx=0, тогда получится, что и sinx=0, а такого быть не может по основному тригонометрическому тождеству
 , и мы можем поделить на него уравнение:
, и мы можем поделить на него уравнение:  ; k - целое число. Есть ещё, кстати, интересный способ для этого уравнения, он применим, называется "метод вспомогательного аргумента", он сложноват, но зато если в правой части НЕ ноль, то тем способом уравнение не решить, а этим - запросто.
; k - целое число. Есть ещё, кстати, интересный способ для этого уравнения, он применим, называется "метод вспомогательного аргумента", он сложноват, но зато если в правой части НЕ ноль, то тем способом уравнение не решить, а этим - запросто.  . Тогда получим:
. Тогда получим:  . Но если это сложно понять сейчас, просто забудь - это способ для решения реально труднорешаемых уравнений.
. Но если это сложно понять сейчас, просто забудь - это способ для решения реально труднорешаемых уравнений.
Ответ: а) k - целое число; б)
k - целое число; б)  k - целое число. в)
k - целое число. в)  k и n - целые числа. г)
k и n - целые числа. г) k и n - целые числа. д)
k и n - целые числа. д) ; k - целое число.
; k - целое число.
P.S. Тебе не нужно писать: "k - целое число", достаточно k∈Z, просто в самом редакторе этого символа я не нашёл, поэтому пришлось писать так, а запись "k∈Z" позволит красиво и понятно объяснить, каким должно являться это число.
2.
3.
4.
5. Предположим, что cosx=0, тогда получится, что и sinx=0, а такого быть не может по основному тригонометрическому тождеству
Ответ: а)
P.S. Тебе не нужно писать: "k - целое число", достаточно k∈Z, просто в самом редакторе этого символа я не нашёл, поэтому пришлось писать так, а запись "k∈Z" позволит красиво и понятно объяснить, каким должно являться это число.
Автор ответа:
0
Прошу прощения за невнимательность. В той строчке, где я начал писать формулу "Метода вспомогательного аргумента" в числителе первого множителя в скобке не "1", там "а"
Автор ответа:
0
спасибо я уже сдал работу получил 5 )))
Автор ответа:
0
Все правильно? Хорошо. Но метод этот сложноват, особенно если путаешься с аркфункциями
Автор ответа:
0
Я про м. вспомогательного аргумета
Автор ответа:
0
аргумента*
Похожие вопросы
Предмет: Музыка,
автор: vladikboy1337
Предмет: Литература,
автор: ivanovaavdirina
Предмет: Математика,
автор: Polina2680
Предмет: Математика,
автор: degovtsovlesha