Предмет: Алгебра,
автор: NB7
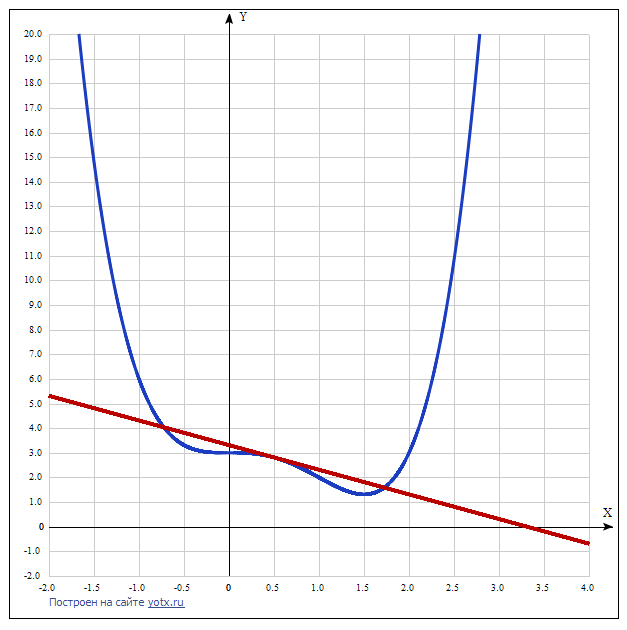
найти угол между касательной к графику функции
y=x^4-2x^3+3 в (.) x0=1/2
Ответы
Автор ответа:
0
Угол между касательной к графику функции и осью х находится по тангенсу этого угла.Тангенс равен первой производной функции в заданной точке.
f(x) = x^4 - 2x^3 + 3.
f'(x) = 4x³ - 6x².
tgα = f'(xo) = 4*(1/2)³ - 6*(1/2)² = (4 / 8) - (6 / 4) = (4 - 12) / 8 = -8 / 8 = -1.
arc tg(-1) = -45°.
Ответ: угол между касательной к графику функции в точке х=0,5 и осью х равен -45°.
f(x) = x^4 - 2x^3 + 3.
f'(x) = 4x³ - 6x².
tgα = f'(xo) = 4*(1/2)³ - 6*(1/2)² = (4 / 8) - (6 / 4) = (4 - 12) / 8 = -8 / 8 = -1.
arc tg(-1) = -45°.
Ответ: угол между касательной к графику функции в точке х=0,5 и осью х равен -45°.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: timofeimordasov942
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: Chuvashov07
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: nadezhdakudrya