Предмет: Геометрия,
автор: Mvfif20032003
50 баллов за решение! Сделайте 125 используя условие 124. Заранее спасибо.
Приложения:

Ответы
Автор ответа:
0
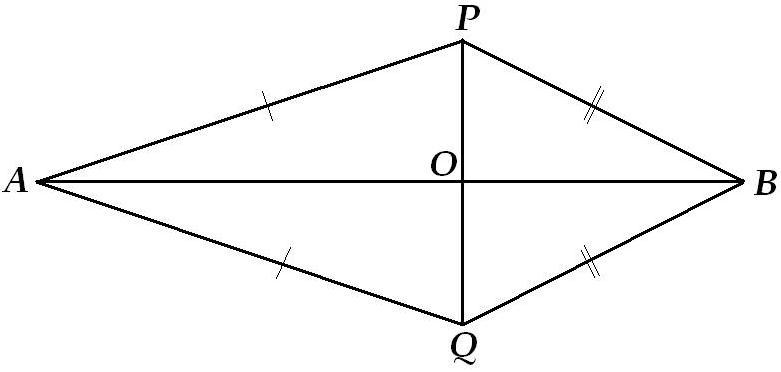
Смотрим рисунок:
ΔAPB=ΔAQB по третьему признаку равенства Δ-ков (AP=AQ, BP=BQ, AB - общая сторона).
Значит ∠PAB=∠QAB и ∠PBA=∠QBA, то есть АВ - биссектриса ∠PBQ и ∠PAQ (таким образом мы доказали 124-е задание).
Теперь рассмотрим ΔPBQ и ΔPAQ: они равнобедренные (по условию AP=AQ, BP=BQ), ВО и АО - их биссектрисы. Так как в равнобедренном треугольнике биссектриса является медианой и высотой, то АВ⊥PQ
ЧТД
ΔAPB=ΔAQB по третьему признаку равенства Δ-ков (AP=AQ, BP=BQ, AB - общая сторона).
Значит ∠PAB=∠QAB и ∠PBA=∠QBA, то есть АВ - биссектриса ∠PBQ и ∠PAQ (таким образом мы доказали 124-е задание).
Теперь рассмотрим ΔPBQ и ΔPAQ: они равнобедренные (по условию AP=AQ, BP=BQ), ВО и АО - их биссектрисы. Так как в равнобедренном треугольнике биссектриса является медианой и высотой, то АВ⊥PQ
ЧТД
Приложения:
Похожие вопросы
Предмет: Литература,
автор: 12345678901754321789
Предмет: Русский язык,
автор: zadaeva06
Предмет: Литература,
автор: isenoggfastan
Предмет: Математика,
автор: 100baby