Question

из точки А и В лежащих в гранях двухграного угла,опущены перпендикуляры АА1 ВВ1 ,на ребро угла.Найдите двухграный угол альфа ,если АА1=3 ВВ1=6,АВ=7

Answer 1

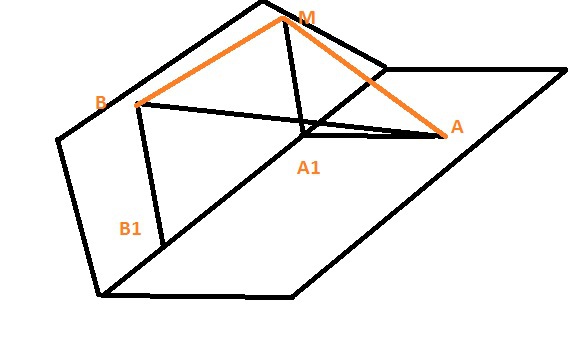
Проведем ВМ // В1А1 и А1М//ВВ1. Получится прямоугольник ВМА1В1.
А1М и АА! перпендикулярны А1В1⇒ А1В1⊥пл АА1М. ВМ//А1В1⇒ВМ⊥пл АА1М. Значит треугольник ВМА - прямоугольный с гипотенузой ВМ.МА=√(ВА²-ВМ²)=√(49-36)=√13.
Теперь рассмотрим треугольник МА1А. ∠А1=α
По теореме косинусов cosα=(A1M²+A1A²-MA²)/(2A1M*A1A)=(16+9-13)/(2*4*3)=12/24=1/2.
∠α= arccos(1/2)=60°. Внимательнее будь при записи условия.

Answer 2

спасибо!))