Предмет: Математика,
автор: dariya1802
Иррациональное уравнение решите, пожалуйста!!! Используя замену t
Заранее СПАСИБО
Приложения:
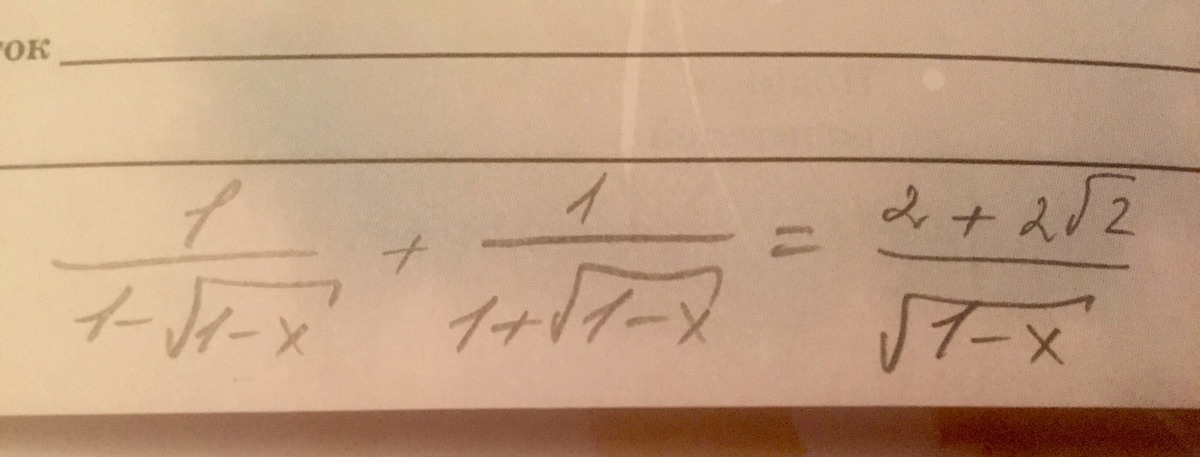
Ответы
Автор ответа:
0
Автор ответа:
0
спасибо!!!
Похожие вопросы
Предмет: Кыргыз тили,
автор: atahanbakirov9
Предмет: Обществознание,
автор: kerakeka
Предмет: Математика,
автор: evatrohimec
Предмет: Математика,
автор: фифи
Предмет: Математика,
автор: viktoriyasobol