Предмет: Геометрия,
автор: rrrrtttt01
В равнобедренном треугольнике большая сторона составляет 75 % суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Ответы
Автор ответа:
0
Треугольник равнобедренный.
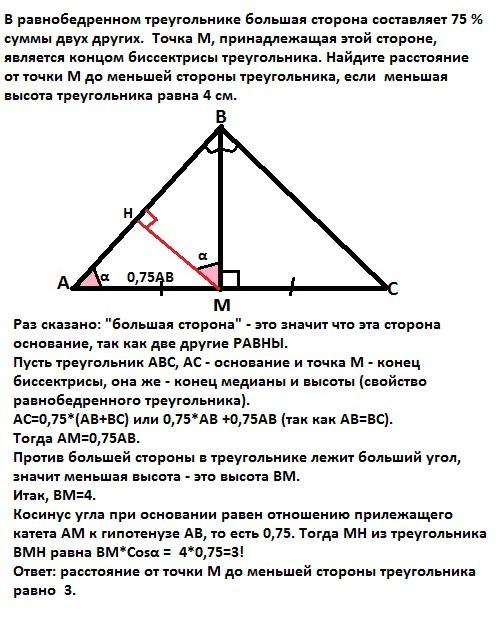
Раз сказано: "большая сторона" - это значит что эта сторона основание, так как две другие РАВНЫ.
Пусть треугольник АВС, АС - основание и точка М - конец биссектрисы, она же - конец медианы и высоты (свойство равнобедренного треугольника).
АС=0,75*(АВ+ВС) или 0,75*АВ +0,75АВ (так как АВ=ВС).
Тогда АМ=0,75АВ.
Против большей стороны в треугольнике лежит больший угол, значит меньшая высота - это высота ВМ.
Итак, ВМ=4.
Косинус угла при основании равен отношению прилежащего катета АМ к гипотенузе АВ, то есть 0,75. Тогда МН из треугольника ВМН равна
МН=BM*Cosα = 4*0,75=3!
Ответ: расстояние от точки М до меньшей стороны треугольника равно 3.
Раз сказано: "большая сторона" - это значит что эта сторона основание, так как две другие РАВНЫ.
Пусть треугольник АВС, АС - основание и точка М - конец биссектрисы, она же - конец медианы и высоты (свойство равнобедренного треугольника).
АС=0,75*(АВ+ВС) или 0,75*АВ +0,75АВ (так как АВ=ВС).
Тогда АМ=0,75АВ.
Против большей стороны в треугольнике лежит больший угол, значит меньшая высота - это высота ВМ.
Итак, ВМ=4.
Косинус угла при основании равен отношению прилежащего катета АМ к гипотенузе АВ, то есть 0,75. Тогда МН из треугольника ВМН равна
МН=BM*Cosα = 4*0,75=3!
Ответ: расстояние от точки М до меньшей стороны треугольника равно 3.
Приложения:
Похожие вопросы
Предмет: География,
автор: lapshinastarhkg
Предмет: Математика,
автор: vvtvm
Предмет: Английский язык,
автор: kostamocalov8
Предмет: Математика,
автор: Дирекшионер77