Предмет: Алгебра,
автор: zere98
ПОМОГИТЕЕЕ ПОЖАЛУЙСТА РЕШИТЬ
Приложения:
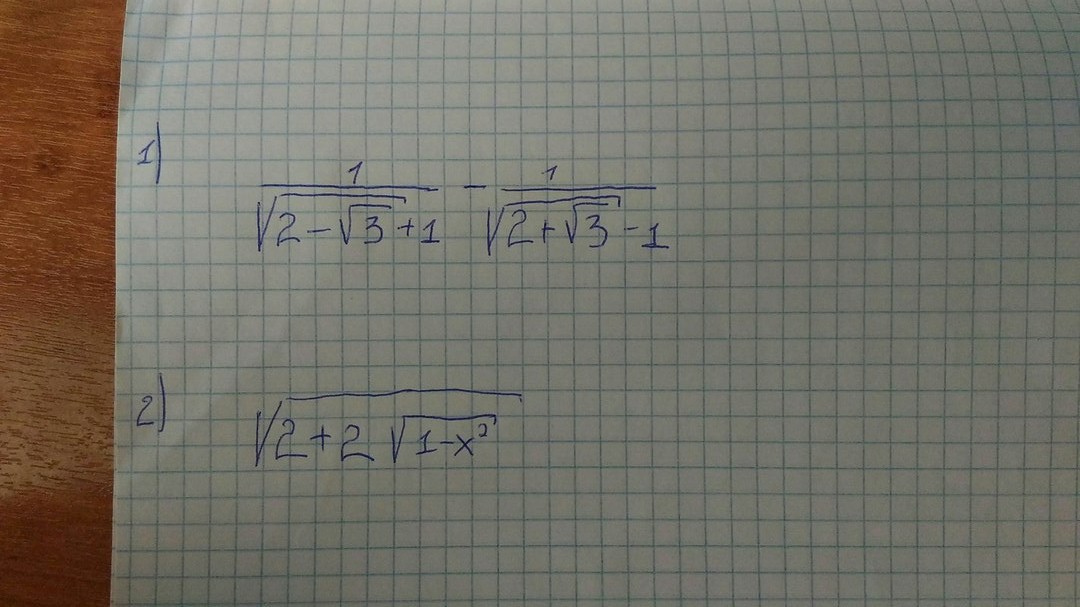
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо Вам большое!только объясните пожалуйста в первом задании,почему во второй дроби в знаменатели у единицы поменялся знак?было минус 1 а потом +1?)
Автор ответа:
0
Да. я сделала описку.Минус по условию надо сохранить. Тогда ответ будет (корень2-2)/(3-корень2).
Похожие вопросы
Предмет: Геометрия,
автор: liza2004674
Предмет: Русский язык,
автор: nurlanovborbu65968
Предмет: Английский язык,
автор: vlkvln3003
Предмет: Математика,
автор: ZEP78
Предмет: Биология,
автор: лизочкаосипова