Предмет: Геометрия,
автор: ymit2
дан выпуклый четырехугольник abcd такой, что ad = ab + cd.Биссектриса угла a проходит через середину стороны bc.Докажите, что биссектриса угла d также проходит через середину bc.
Ответы
Автор ответа:
0
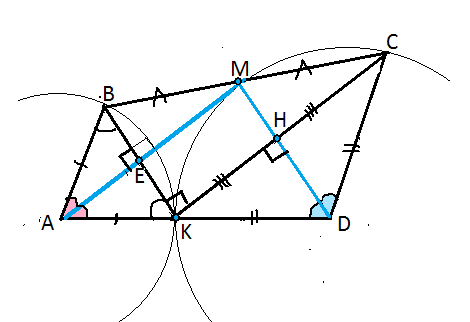
Чтобы рисунок соответствовал условию задачи, воспользуемся для его построения окружностями с центром в точке А и радиусом АВ,
и с центром в точке D и радиусом СD.
Обозначим середину ВС буквой М.
Нужно доказать, что биссектриса угла D пересекает ВС в точке М.
По условию АD=АВ+СD, следовательно, АВ=АК, КD=СD
Треугольник АВК равнобедренный, АЕ - биссектриса, ⇒
АЕ- ещё и высота, и медиана.
Высота треугольника перпендикулярна стороне, к которой проведена⇒
угол ВЕА=∠АЕК=90º.
Δ АDС равнобедренный, биссектриса DН- его высота и медиана. ⇒
угол СНD=∠КНD=90º.
В треугольнике КВС отрезки ВМ=МС по условию
КН=НС, т.к. DН - медиана,
ВЕ=ЕК, т.к. АЕ - медиана⇒
МН - средняя линия. и ЕМ- средняя линия
ЕМ=КН, МН=ЕК, ⇒
МН||ВК и
ЕМ||КН
∠МЕК=90º как смежный с ∠AEK, поэтому
∠ЕМН=90º как соответственный ∠ВЕМ при прямых MH||ВК и секущей МЕ.
Четырехугольник ЕМНК - прямоугольник. .
Через одну точку на прямой можно провести только один перпендикуляр. ⇒
НМ - продолжение DН. ⇒
Биссектриса DМ угла D проходит через середину стороны ВС, ч.т.д.
и с центром в точке D и радиусом СD.
Обозначим середину ВС буквой М.
Нужно доказать, что биссектриса угла D пересекает ВС в точке М.
По условию АD=АВ+СD, следовательно, АВ=АК, КD=СD
Треугольник АВК равнобедренный, АЕ - биссектриса, ⇒
АЕ- ещё и высота, и медиана.
Высота треугольника перпендикулярна стороне, к которой проведена⇒
угол ВЕА=∠АЕК=90º.
Δ АDС равнобедренный, биссектриса DН- его высота и медиана. ⇒
угол СНD=∠КНD=90º.
В треугольнике КВС отрезки ВМ=МС по условию
КН=НС, т.к. DН - медиана,
ВЕ=ЕК, т.к. АЕ - медиана⇒
МН - средняя линия. и ЕМ- средняя линия
ЕМ=КН, МН=ЕК, ⇒
МН||ВК и
ЕМ||КН
∠МЕК=90º как смежный с ∠AEK, поэтому
∠ЕМН=90º как соответственный ∠ВЕМ при прямых MH||ВК и секущей МЕ.
Четырехугольник ЕМНК - прямоугольник. .
Через одну точку на прямой можно провести только один перпендикуляр. ⇒
НМ - продолжение DН. ⇒
Биссектриса DМ угла D проходит через середину стороны ВС, ч.т.д.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: elina06sp
Предмет: Геометрия,
автор: maksim365869
Предмет: Другие предметы,
автор: botatanatar
Предмет: Математика,
автор: dana807
Предмет: Обществознание,
автор: Kristinavolwom