Предмет: Алгебра,
автор: batya07
CДЕЛАЙТЕ ПОЖАЛУЙСТА НОМЕР 170 В,171 В,Г,172,А,Б!
Приложения:
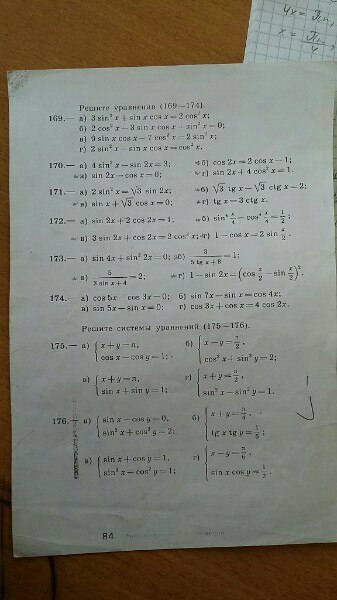
Ответы
Автор ответа:
0
170(в)
2sinxcosx-cosx=0
cosx(2sinx-1)=0
sinx=0⇒x=πn,n∈Z
sinx=1/2⇒x=(-1)^n*π/6+πk,k∈z
171(в)
sinx+√3cosx=0
2(1/2sinx+√3/2cosx)=0
2(sinxcosπ/3+cosxsinπ/3)=0
2sin(x+π/3)=0
x+π/3=πn,n∈z
x=-π/3+πn,n∈z
171(г)
tgx-3/tgx=0
tg²x-3=0
(tgx-√3)(tgx+√3)=0
tgx=√3⇒x=π/3+πn,n∈z
tgx=-√3⇒x=-π/3+πk,k∈z
172(а)
2sinxcosx+2cos²x-2sin²x-sin²x-cos²x=0
3sin²x-2sinxcosx-cos²x=0/cos²x
3tg²x-2tgx-1=0
tgx=a
3a²-2a-1=0
D=4+12=16
a1=(2-4)/6=-1/3⇒tgx=-1/3⇒x=-arctg1/3+πn,n∈z
a2=(2+4)/6=1⇒tgx=1⇒x=π/4+πk,k∈z
172(б)
(sin²x/4-cos²x/4)(sin²x/4+cos²x/4)=1/2
sin²x/4-cos²x/4=1/2
(1-cosx/2)/2-(1+cosx/2)/2=1/2
1-cosx/2-1-cosx/2=1
-2cosx/2=1
cosx/2=-1/2
x/2=+-2π/3+2πn,n∈z
x=+-4π/3+4πn,n∈z
2sinxcosx-cosx=0
cosx(2sinx-1)=0
sinx=0⇒x=πn,n∈Z
sinx=1/2⇒x=(-1)^n*π/6+πk,k∈z
171(в)
sinx+√3cosx=0
2(1/2sinx+√3/2cosx)=0
2(sinxcosπ/3+cosxsinπ/3)=0
2sin(x+π/3)=0
x+π/3=πn,n∈z
x=-π/3+πn,n∈z
171(г)
tgx-3/tgx=0
tg²x-3=0
(tgx-√3)(tgx+√3)=0
tgx=√3⇒x=π/3+πn,n∈z
tgx=-√3⇒x=-π/3+πk,k∈z
172(а)
2sinxcosx+2cos²x-2sin²x-sin²x-cos²x=0
3sin²x-2sinxcosx-cos²x=0/cos²x
3tg²x-2tgx-1=0
tgx=a
3a²-2a-1=0
D=4+12=16
a1=(2-4)/6=-1/3⇒tgx=-1/3⇒x=-arctg1/3+πn,n∈z
a2=(2+4)/6=1⇒tgx=1⇒x=π/4+πk,k∈z
172(б)
(sin²x/4-cos²x/4)(sin²x/4+cos²x/4)=1/2
sin²x/4-cos²x/4=1/2
(1-cosx/2)/2-(1+cosx/2)/2=1/2
1-cosx/2-1-cosx/2=1
-2cosx/2=1
cosx/2=-1/2
x/2=+-2π/3+2πn,n∈z
x=+-4π/3+4πn,n∈z
Похожие вопросы
Предмет: История,
автор: katysha9987
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: RiksterTop
Предмет: Математика,
автор: arturglebov
Предмет: Алгебра,
автор: Лауритта280114