Предмет: Алгебра,
автор: vetrovaksenia2
lod0.2(-x^2+4x+5)=log0.2(-x-31)
(см. опис.)
Приложения:
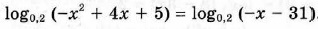
Ответы
Автор ответа:
0
Решение
log₀,₂ (- x² + 4x + 5) = log₀,₂ (- x - 31)
- x² + 4x + 5 = - x - 31
x² - 5x - 36 = 0
x₁ = - 4
x₂ = 9
Проверка
x₁ = - 4
Л.ч log₀,₂ (- x² + 4x + 5) = log₀,₂ [- (-4)² + 4*(-4) + 5] =
= log₀,₂ (- 16 - 16 + 5) = log₀,₂ (-27)
П.ч. log₀,₂ (- x - 31) = log₀,₂ (- (-4) - 31= log₀,₂ (- 27)
log₀,₂ (-27) = log₀,₂ (-27) верно
x₂ = 9
Л.ч. log₀,₂ (- x² + 4x + 5) = log₀,₂ (- 9² + 4*9 + 5) = log₀,₂ ( - 40)
П.ч. log₀,₂ (- x - 31) = log₀,₂ (- 9 - 31) = log₀,₂ (- 40)
log₀,₂ (- 40) = log₀,₂ (- 40) верно
Ответ: x₁ = - 4 ; x₂ = 9
log₀,₂ (- x² + 4x + 5) = log₀,₂ (- x - 31)
- x² + 4x + 5 = - x - 31
x² - 5x - 36 = 0
x₁ = - 4
x₂ = 9
Проверка
x₁ = - 4
Л.ч log₀,₂ (- x² + 4x + 5) = log₀,₂ [- (-4)² + 4*(-4) + 5] =
= log₀,₂ (- 16 - 16 + 5) = log₀,₂ (-27)
П.ч. log₀,₂ (- x - 31) = log₀,₂ (- (-4) - 31= log₀,₂ (- 27)
log₀,₂ (-27) = log₀,₂ (-27) верно
x₂ = 9
Л.ч. log₀,₂ (- x² + 4x + 5) = log₀,₂ (- 9² + 4*9 + 5) = log₀,₂ ( - 40)
П.ч. log₀,₂ (- x - 31) = log₀,₂ (- 9 - 31) = log₀,₂ (- 40)
log₀,₂ (- 40) = log₀,₂ (- 40) верно
Ответ: x₁ = - 4 ; x₂ = 9
Похожие вопросы
Предмет: История,
автор: zaneginda
Предмет: Окружающий мир,
автор: nat48355799
Предмет: Биология,
автор: kseroman
Предмет: Биология,
автор: anastasya0999