Предмет: Алгебра,
автор: FoxtrotALT
Решите любой, пожалуйста Логарифмические неравенства
Приложения:
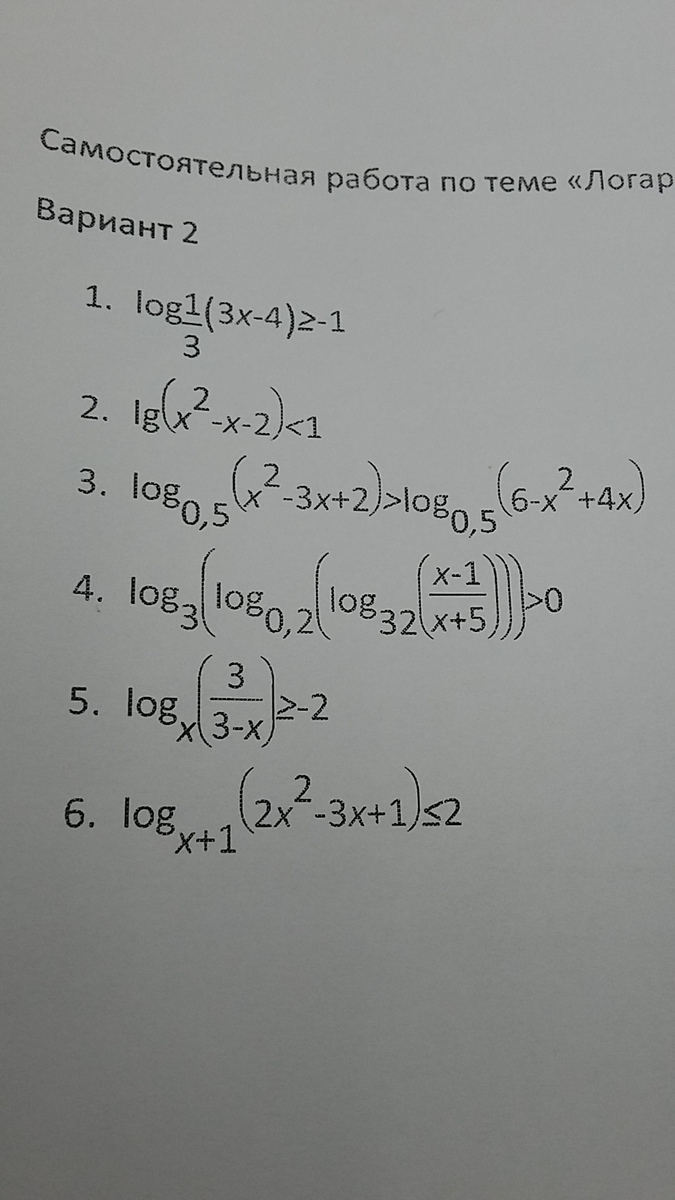
Ответы
Автор ответа:
0
Решение
log₁/₃ (3x - 4) ≥ - 1
ОДЗ: 3x - 4 > 0, x > 4/3, x ∈ (4/3 ; + ∞)
так как 0 < 1/3 < 1, то
3x - 4 ≤ (-1/3)⁻¹
3x - 4 ≤ - 3
3x ≤ 1
x ≤ 1/3
x ∈ (- ∞ 1/3] не принадлежит ОДЗ x ∈ (4/3 ; + ∞)
Ответ: решений нет
log₁/₃ (3x - 4) ≥ - 1
ОДЗ: 3x - 4 > 0, x > 4/3, x ∈ (4/3 ; + ∞)
так как 0 < 1/3 < 1, то
3x - 4 ≤ (-1/3)⁻¹
3x - 4 ≤ - 3
3x ≤ 1
x ≤ 1/3
x ∈ (- ∞ 1/3] не принадлежит ОДЗ x ∈ (4/3 ; + ∞)
Ответ: решений нет
Похожие вопросы
Предмет: Биология,
автор: besovoleg2019
Предмет: Геометрия,
автор: daria09119284
Предмет: Другие предметы,
автор: viktoriya291007
Предмет: Физика,
автор: garaeva2000