Предмет: Геометрия,
автор: ОченьСложна
Дан прямой параллелепипед ABCDA1B1C1D1, основание которого - квадрат. Точка О - точка пересечения диагоналей грани ABCD. Сумма длин бокового ребра и стороны основания равна 9 см. Вычислите площадь боковой грани призмы ABCDA1B1D1 , если площадь треугольника AOB равна 4 см*2
Ответы
Автор ответа:
0
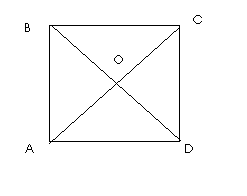
Диагонали квадрата разбивают его на 4 равных прямоугольных треугольника ( см. рисунок в приложении)
S(квадрата)= 4 S(Δ AOB)=4·4=16 cм²
S(квадрата)= а²
а²=16 ⇒ а = 4 см
По условию "сумма длин бокового ребра и стороны основания равна 9 см", значит боковое ребро равно 9-4=5 см
S(AA₁B₁B)=S(BB₁C₁C)=S(CC₁D₁D)=S(DD₁A₁A)=4·5=20 cм²
Ответ. 20 кв. см
S(квадрата)= 4 S(Δ AOB)=4·4=16 cм²
S(квадрата)= а²
а²=16 ⇒ а = 4 см
По условию "сумма длин бокового ребра и стороны основания равна 9 см", значит боковое ребро равно 9-4=5 см
S(AA₁B₁B)=S(BB₁C₁C)=S(CC₁D₁D)=S(DD₁A₁A)=4·5=20 cм²
Ответ. 20 кв. см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: aaldiyar2903
Предмет: Алгебра,
автор: anavasilevskaa51
Предмет: Английский язык,
автор: Symbatkabat
Предмет: Геометрия,
автор: ксенсергеевна