Предмет: Геометрия,
автор: vaiti
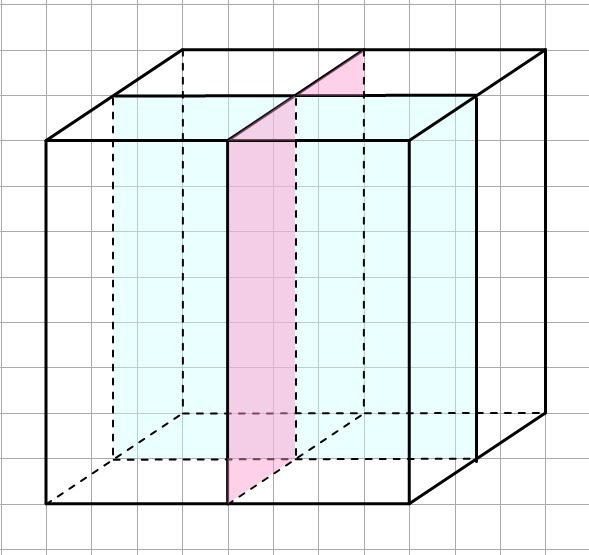
Деревянный брусок, имеющий форму куба, распилили на четыре части, каждая из которых имеет форму прямоугольного параллелепипеда. Основаниями этих частей
служат равные квадраты, площадь каждого из которых равна 4 см^2. Вычислите площадь боковой поверхности полученной модели прямоугольного параллелепипеда.
Ответы
Автор ответа:
0
Так как площадь оснований полученных частей 4 см², то их основание имеет размеры 2х2 см, а сам куб имеет размеры 4х4х4 см.
При разделении данного куба на 4 части образуется 4 одинаковых прямоугольных параллелепипеда с основанием, равным по площади четверти основания куба и высотой, равной высоте куба.
Площадь боковой поверхности одного такого параллелепипеда:
S = 4S₂, где S₂ - площадь боковой грани
Тогда: S = 4*4*2 = 32 (см²)
Ответ: 32 см²
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Русский язык,
автор: saparbaevabalkynaj
Предмет: Геометрия,
автор: oleg1234123123123123
Предмет: Алгебра,
автор: leonich2014
Предмет: Математика,
автор: madamanfica