Предмет: Алгебра,
автор: comblrrr
Решите уравнение по алгебре 11 класс, пожалуйста
Приложения:
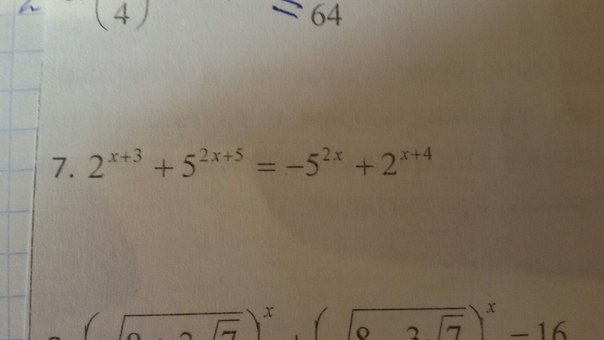
Ответы
Автор ответа:
0
Автор ответа:
0
Там же в скобках где 5^(2x)*(5^5+1) должно 3125+1=3126 получиться
Автор ответа:
0
Спасибо большое!
Автор ответа:
0
Числа, конечн получились некрасивые, но такое условие..
Похожие вопросы
Предмет: Музыка,
автор: bekzanovaglzada
Предмет: История,
автор: antonetsanhelina
Предмет: Английский язык,
автор: anymm
Предмет: Информатика,
автор: margorita201
Предмет: Алгебра,
автор: Аноним