Предмет: Алгебра,
автор: Ekatherina
4cos^2 6x+16cos^2 3x=13,
Ответы
Автор ответа:
0
Решение во вложениях...
Приложения:
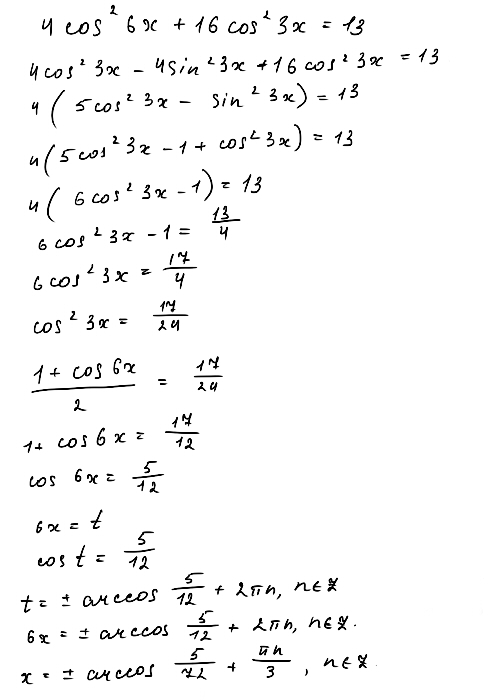
Автор ответа:
0
Замена: cos 6x = t ∈ [-1, 1]
Автор ответа:
0
Применим формулу понижения степени
Решаем уравнение как квадратное уравнение относительно cos6x
D = b² - 4ac = 8² + 4 * 4 * 5 = 144
Похожие вопросы
Предмет: География,
автор: zhandosaykerim90
Предмет: Русский язык,
автор: anazavodskih
Предмет: Русский язык,
автор: natatmcr
Предмет: Математика,
автор: KRISTINA6
Предмет: Математика,
автор: Владик2002