Question

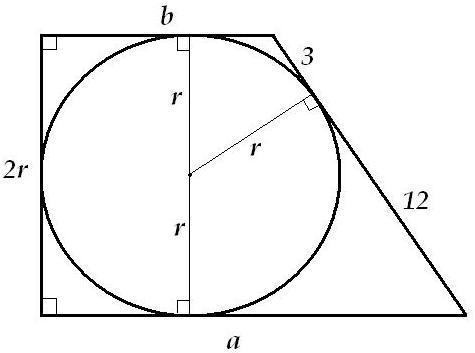
Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 3 и 12 см . Найдите радиус вписанной окружности , если периметр трапеции, равен 54 см

Answer 1

Смотрим рисунок:
Вполне логично, что вторая боковая сторона (с прямыми углами к основаниям) равна 2r.
Теперь вспоминаем свойство трапеции:
В трапецию можно вписать окружность только тогда, когда сумма длин оснований трапеции равна сумме длин её боковых сторон:
$(a+b)=(2r+15)\P=(a+b)+(2r+15)=(2r+15)+(2r+15)=4r+30\4r+30=54$
Продолжать надо?..
$4r=54-30\4r=24\r=6 cm$

Answer 2

спасибо , если можно продолжите пожалуйста , а то тему не понимаю , а надо решить

Answer 3

Уравнение, которое классе 3-м проходят ты решить не можешь?...