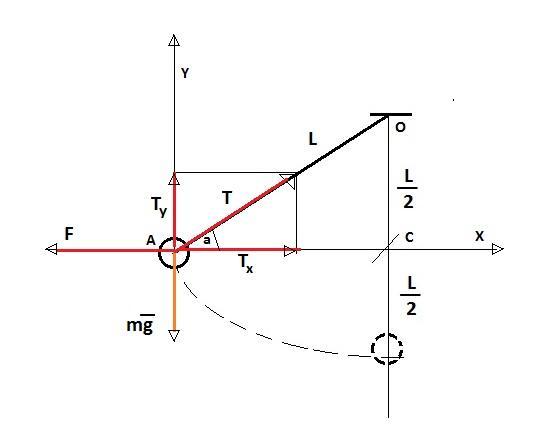
шарик массой 100г подвешен на нити длиной 1м. шарик раскручивают так, что он движется по окружности в горизонтальной плоскости, отстоящей от точки подвеса на половину длины нити. какую работу надо совершить для его раскручивания?
Ответы
Если силой трения пренебрегаем, то необходимо затратить энергию на подъем шарика на высоту l/2 и задания ему скорости v вращения по окружности.
A=mgl/2 +mv^2/2
Шарик будет вращаться за счет центростремительной силой, которая будет создана проекцией реакции опоры на плоскость вращения(она же сила натяжения нити)
mg=N*sina
sina=l/2*l = 1/2
mg=N/2
N=2mg
ma=N*cosa
cosa=корень(1-1/4) = корень(3)/2
a=v^2/R
R^2=l^2-l^2/4 = 3l^2/4
подставляем, решаем
Ответ A=5mgl/4
A=mgl/2+mv^2/2
N=2mg
ma=N*cosA
a=v^2/R
A=5mgl/4
Ответ:
Объяснение:
Дано:
m = 100 г = 0,100 кг
h = L/2
___________
A - ?
1)
Необходимо совершить работу, чтобы поднять шарик из положения равновесия на высоту h=L/2
A₁ = m·g·h = (1/2)·m·g·L
и сообщить шарику кинетическую энергию Ek.
2)
Из чертежа:
Ty = mg
Tx = F (Здесь F - центробежная сила)
tg α = Ty/Tx = mg / F
Но угол α = 30° (поскольку катет OC=L/2 в 2 раза меньше гипотенузы AO=L)
Тогда
F = mg/tg30° (1)
Найдем R = AC = √ (L² - (L/2)²) = (√3/2)·L
Но F по модулю равна центростремительной силе:
F = m·V²/R (2)
Приравняем (2) и (1)
m·V²/R = m·g/tg 30°
m·V² = m·g·R/tg 30°
Разделим на 2:
m·V²/2 = m·g·R/(2·tg30°)
Eк = m·g·R/(2·tg 30°) = m·g·L·√3·3 / (2·√3) = (3/2)m·g·L - кинетическая энергия.
Суммарная работа:
A = A₁+Ek
A = (1/2)·m·g·L+(3/2)m·g·L = 2m·g·L
A = 2·0,1·10·1 = 2 Дж