Предмет: Алгебра,
автор: povadiana9
ОБЪЯСНИТЕ КАК РЕШАТЬ 8 КЛАСС
Приложения:
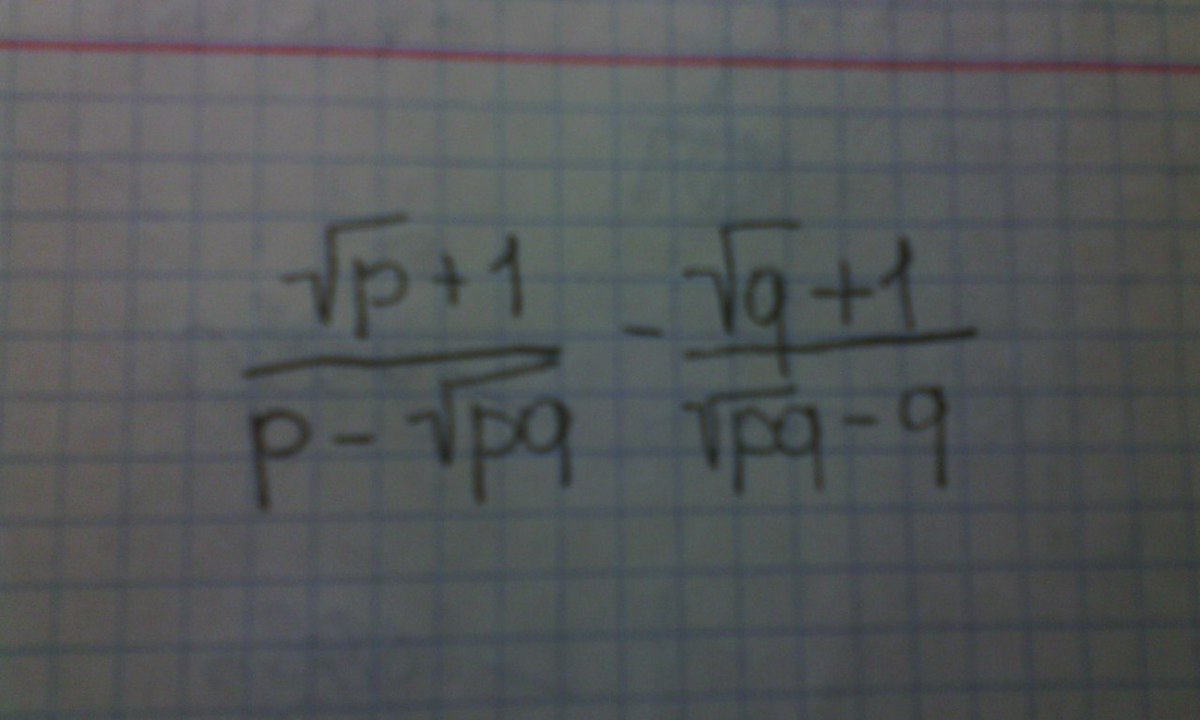
Ответы
Автор ответа:
0
Автор ответа:
0
(√р +1)/(р - √рq) - (√q +1)/(√рq - q)
(р - √рq)= √р(√р - √q) (√рq - q)= √q(√р - √q)
дальше решение смотрите в приложении.
(р - √рq)= √р(√р - √q) (√рq - q)= √q(√р - √q)
дальше решение смотрите в приложении.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: olzhiklion180519
Предмет: Биология,
автор: aniaduynova
Предмет: Математика,
автор: alisa5555630
Предмет: Математика,
автор: Scorpio13
Предмет: Математика,
автор: ozornina1982