Предмет: Алгебра,
автор: kaktyslolda
НАЙТИ НАИБОЛЬШЕЕ ЗНАЧЕНИЕ
y=x(2x-3)^6 на отрезке |x-1/5| <(или равно)0.5
Приложения:
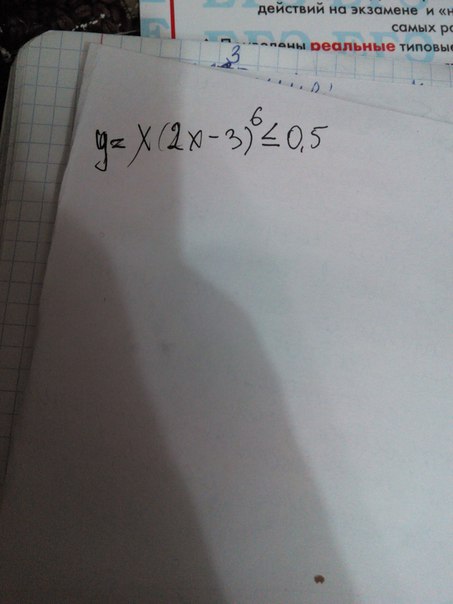
Ответы
Автор ответа:
0
y=x(2x-3)⁶ на отрезке |x-1/5| ≤ 0.5
- 0,5 ≤ x - 0,2 ≤ 0,5
- 0,5 + 0,2 ≤ x ≤ 0,5 + 0,2
- 0,3 ≤ x ≤ 0,7
Решение
Находим первую производную функции:
y' = 12x(2x - 3)⁵ + (2x - 3)⁶
или
y' = (2x - 3)⁵(14x - 3)
Приравниваем ее к нулю:
(2x - 3)⁵(14x - 3) = 0
14x - 3 = 0
x₁ = 3/14
2x - 3 = 0
x₂ = 3/2
Вычисляем значения функции:
f(3/4) = (51018336) / (823543)
f(3/2) = 0
Ответ: fmin = 0; fmax = (51018336) / (823543)
- 0,5 ≤ x - 0,2 ≤ 0,5
- 0,5 + 0,2 ≤ x ≤ 0,5 + 0,2
- 0,3 ≤ x ≤ 0,7
Решение
Находим первую производную функции:
y' = 12x(2x - 3)⁵ + (2x - 3)⁶
или
y' = (2x - 3)⁵(14x - 3)
Приравниваем ее к нулю:
(2x - 3)⁵(14x - 3) = 0
14x - 3 = 0
x₁ = 3/14
2x - 3 = 0
x₂ = 3/2
Вычисляем значения функции:
f(3/4) = (51018336) / (823543)
f(3/2) = 0
Ответ: fmin = 0; fmax = (51018336) / (823543)
Похожие вопросы
Предмет: Физика,
автор: hahlovam06
Предмет: Английский язык,
автор: hfjfjfhhvvvk
Предмет: Русский язык,
автор: ruslanbaleshev04
Предмет: Математика,
автор: katya12882
Предмет: Математика,
автор: lizadolgikh21