Предмет: Геометрия,
автор: Art01
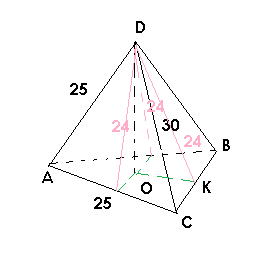
Два боковых ребра треугольной пирамиды равны 25 см и 30 см, а заключенная между ними сторона основания равна 25 см. Найти две другие стороны основания, если площадь боковой поверхности пирамиды равна 840 см2 и высота проходит через центр вписанной в основание окружности.
Ответы
Автор ответа:
0
См. рисунок в приложении.
1) Так как высота пирамиды проходит через центр вписанной окружности, то апофемы боковых граней равны ( равные проекции имеют равные наклонные)
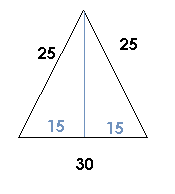
2) Найдем высоту ( апофему боковой грани)равнобедренного треугольника АDС со сторонами 25; 25 и 30 ( см. рисунок 2)
Проведем высоту к основанию 30. По теореме Пифагора эта высота равна
√(25²-15²)=√400=20
1/2·30·20=1/2·25·h ⇒ h ( апофема) =600:25=24
3) S(бок. пирамиды)=(АВ+ВС+АС)·h/2
(АВ+ВС+25)·24/2=840 ⇒ АВ+ВС+25=1680:24 ⇒ АВ+ВС=70-25
АВ+ВС=45
Больше ничего найти не могу. Не хватает данных
может быть одна сторона 25, другая 20.
1) Так как высота пирамиды проходит через центр вписанной окружности, то апофемы боковых граней равны ( равные проекции имеют равные наклонные)
2) Найдем высоту ( апофему боковой грани)равнобедренного треугольника АDС со сторонами 25; 25 и 30 ( см. рисунок 2)
Проведем высоту к основанию 30. По теореме Пифагора эта высота равна
√(25²-15²)=√400=20
1/2·30·20=1/2·25·h ⇒ h ( апофема) =600:25=24
3) S(бок. пирамиды)=(АВ+ВС+АС)·h/2
(АВ+ВС+25)·24/2=840 ⇒ АВ+ВС+25=1680:24 ⇒ АВ+ВС=70-25
АВ+ВС=45
Больше ничего найти не могу. Не хватает данных
может быть одна сторона 25, другая 20.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: dianasuturina2008
Предмет: География,
автор: oljasakzhlov
Предмет: Математика,
автор: adina271146
Предмет: Биология,
автор: жека1101