Предмет: Алгебра,
автор: aisulu000
249 помогите пожалуйста)))
Приложения:
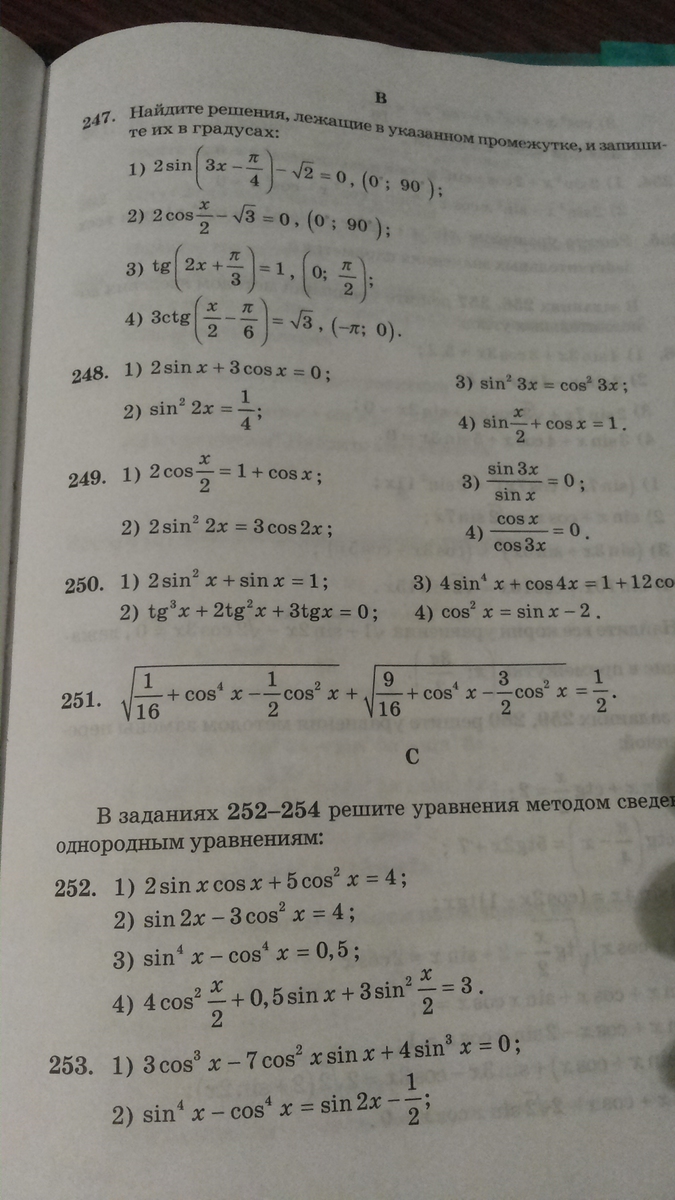
Ответы
Автор ответа:
0
2cos(x/2) = 1+(cos²(x/2)-sin²(x/2)) разложили по формуле cos двойного угла
2cos (x/2)=1+cos²(x/2)-1+cos(x/2) заменили sin²(x/2)=1-cos²(x/2)
2cos²(x/2)- 2cos(x/2)=0
cos²(x/2)-cos(x/2)=0
cos(x/2)(cos(x/2)-1)=0
cos(x/2)=0 или cos(x/2)=1,
x/2 =π/2+πn x/2 =2πn
x=π+2πn x=4πn
2cos (x/2)=1+cos²(x/2)-1+cos(x/2) заменили sin²(x/2)=1-cos²(x/2)
2cos²(x/2)- 2cos(x/2)=0
cos²(x/2)-cos(x/2)=0
cos(x/2)(cos(x/2)-1)=0
cos(x/2)=0 или cos(x/2)=1,
x/2 =π/2+πn x/2 =2πn
x=π+2πn x=4πn
Автор ответа:
0
спасибо. но я начала не поняла, можете объяснить?
Автор ответа:
0
есть формула косинус двойного угла, так вот сначала 1+cosx запиши, как 1+cos2*(x/2) то есть х=2* х/2
Автор ответа:
0
тогда cos 2* x/2 = cos в квадрате х/2 - sin в квадрате х/2
Автор ответа:
0
спасибо
Автор ответа:
0
3 и 4 помогите пожалуйста!!)))))
Похожие вопросы
Предмет: Музыка,
автор: vikadavydova2007
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: umarkanybekov090110
Предмет: Алгебра,
автор: poet2015