Предмет: Геометрия,
автор: pozelovv
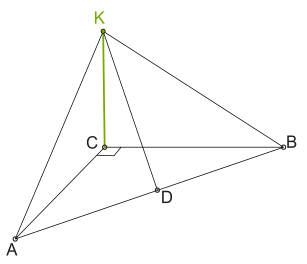
Через вершину прямого угла C к плоскости прямоугольного треугольника ABC проведена перпендикулярная прямая KC.
Точка D делит пополам гипотенузу AB.
Длина катетов треугольника AC = 42 мм и BC = 56 мм.
Расстояние KC = 12 мм. Рассчитай расстояние KD.
Приложения:
Ответы
Автор ответа:
0
Найдем медиану СД;
Она будет равна АД и ДВ, по условию, так как точка Д -центр описанной окружности прямоугольного треугольника.Значит СД=АВ/2=70/2=35;
А так как треугольник КСД по условию тоже прямоугольный,то КД НАХОДИМ ПО Т-ме Пифагора:КД^2=КС^2+СД^2=144+1225=1369;
КД=37;
Ответ:КД=37.
Откуда
Автор ответа:
0
медиана не СК, а СД. и равна она будет не СД и ДВ, а АД и ДВ. Исправьте.
Автор ответа:
0
ответ то правильный?
Автор ответа:
0
Да, правильный.
Автор ответа:
0
Спасибо!!!
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ajtorezamagat24
Предмет: Математика,
автор: strelnikova0910
Предмет: Обществознание,
автор: zhannurkanatova5
Предмет: География,
автор: мартинова
Предмет: Литература,
автор: золорапне