Предмет: Алгебра,
автор: nastyasherbako
Помогите решить систему!!!! Очень надо! Задание во вложениях!
Приложения:
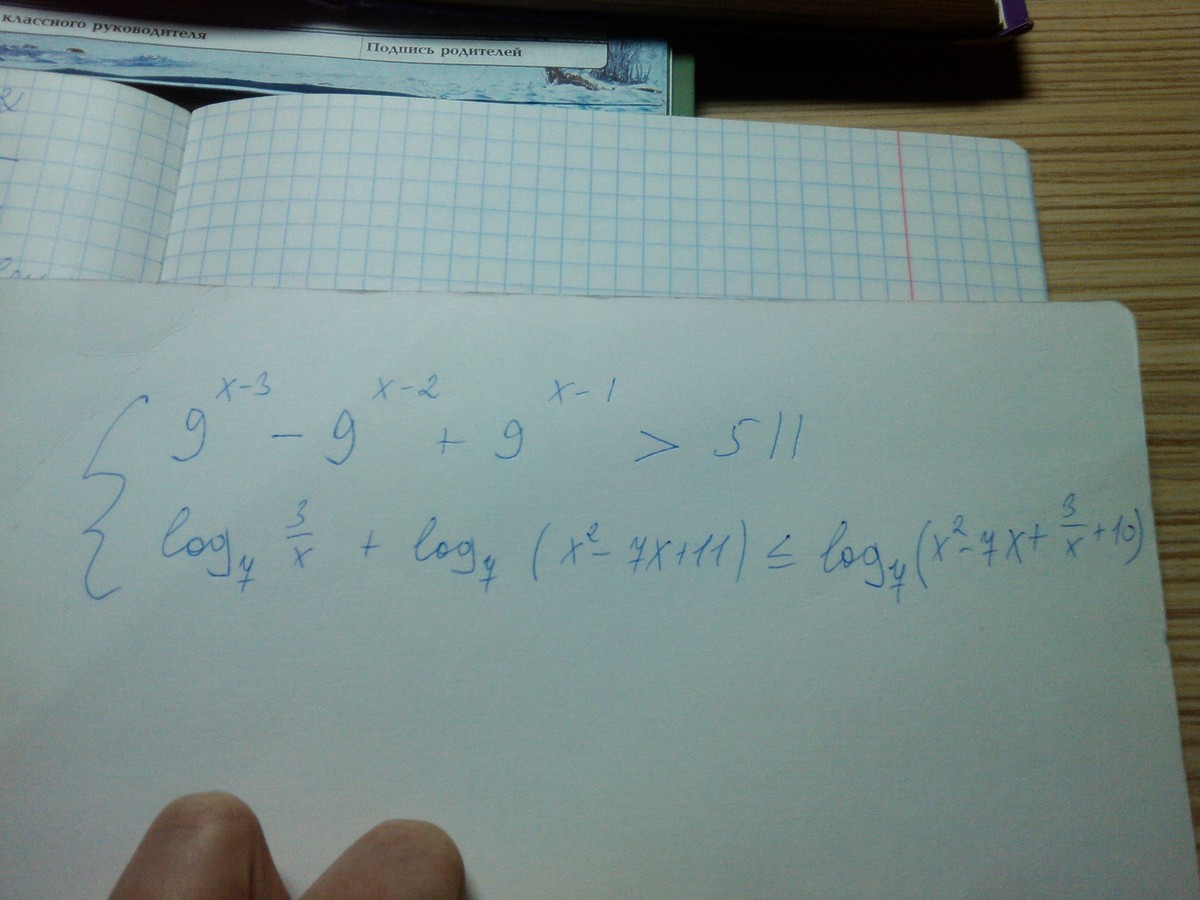
Ответы
Автор ответа:
0
кубическое уравнение решаем по теореме Безу
теперь делим уголком это уравнение на x=2 => x-2 после чего получаем следующее
Это надо ещё совместить с ОДЗ
а также нужно совместить с первым решением
и в итоге выходит
Похожие вопросы
Предмет: Английский язык,
автор: 676456884
Предмет: Математика,
автор: nurgaliyevaasel09
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: Kadra
Предмет: Алгебра,
автор: Whut