№1
стороны треугольника равны 6 см, 25см, 29 см. Найти радиусы вписанной и описанной окружностей и высоту к меньшей стороне треугольника.
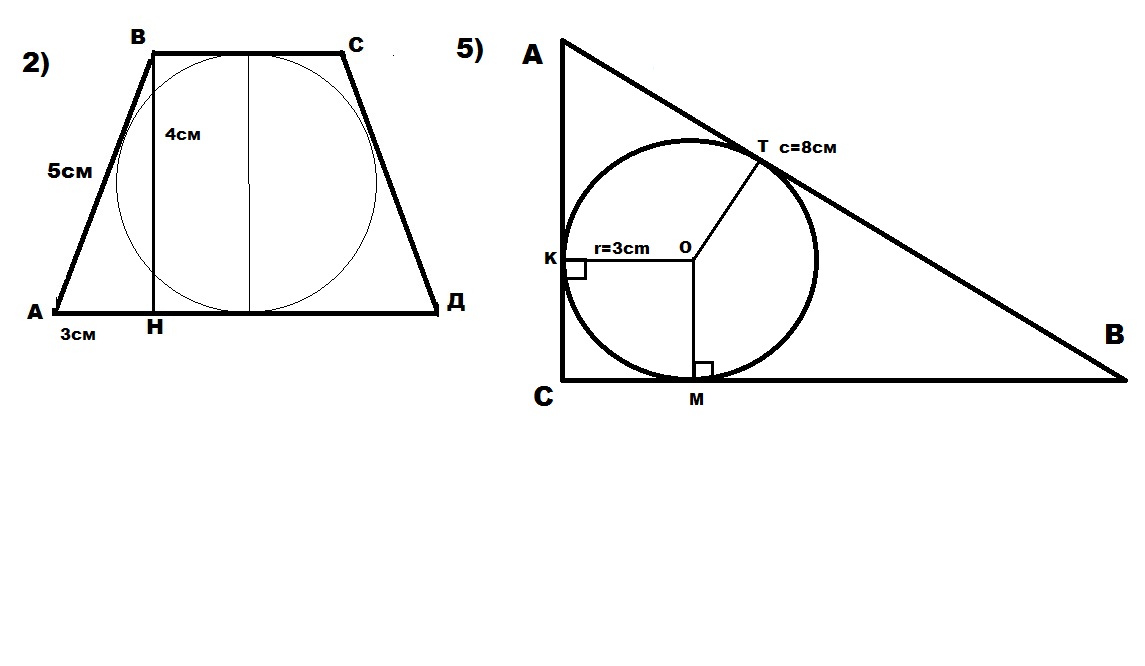
№2
Боковая сторона равнобедренной трапеции 5 см, радиус вписанной в нее окружности 2 см. Найти основания трапеции.
№3
Сторона ромба 25 см, меньшая диагональ 14 см. Найти радиус окружности вписанной в ромб.
№4
Катеты прямоугольного треугольника относятся 5:12. R-r=18
Найти R и r.
№5
Гипотенуза прямоугольного треугольника равна 8, а радиус окружности вписанной в него 3. Найти площадь треугольника.
Ответы
следующий раз задавай задачи по 1-2, а то долгл всех ждать
1) ha= ( 1/2 * sqrt p (p−a) (p−b) (p−c) ) / a ha=20cm
r= (sqrt(p−a)(p−b)(p−c)) / p r=2cm
R= abc / ( 4 sqrt (p(p−a)(p−b)(p−c) ) R= 18 1/4 cm
2) r= h / 2 h= 2r h=4cm
рассмотрим АВН-прямоугольный египетский ( ВН -высота) , т.е соотношение сторон 3: 4: 5 АН=3см
В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.: AB+DC= AD+BC = 10см
пусть ВС=х см х +(3+х+3 )= 10см х=2см
BC = 2см AD =8см 3) АВСД= ромб d1=14cm a =25cm, находим d2 = 24*2=48cm r= sqrt ( (d1/2)^2 +( d2/2)^2) r=12cm 4)ABC -прямоугольный С=90* АС=12х ВС=5х по тПифагора АВ=13х R-r = 18cm r=sqrt ( ((p−a)(p−b)(p−c) / p ) r=2x R= 1 / 2 sqrt (a^2+ b^2) R=6.5x R-r=4.5x=18 x= 4 => R=6.5 * 4=26cm r=2 * 4=8cm 5) S=1/2a*b c=8cm, r=3см проведем OT,ОМ и ОК -радиусы к точкам касания, ОМ_|_CB OT_|_AB OK_|_AC => CM=CK=r=3cm по свойству касательных из одной точки к окр АК=АТ ВТ=ВМ , пусть АТ=х тогда ТВ=8-х дальше легко, давай сам