Question

Помогите решить 240(б) 279

Answer 1

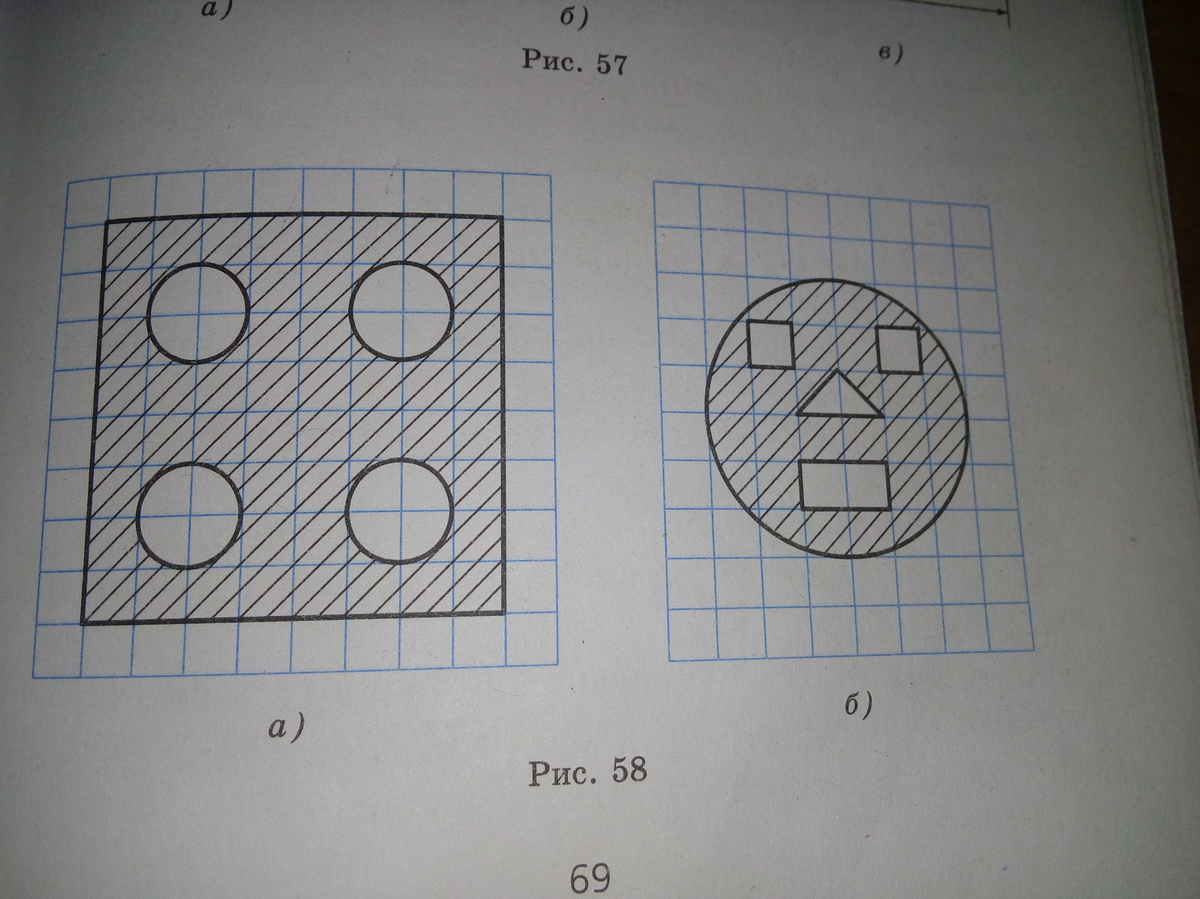
240 б) см рисунок в приложении
R=3a
S(круга)=π·(3а)²=9πа²
S(незаштрихованной части)=S(4-x квадратов)+S(2-x треугольников)=S(5-ти квадратов)=5а²
S(заштрихованной части)=9πа²-5а²=(9π-5)·а²

279.
Cм рисунок 2 в приложении
Пусть стороны прямоугольника а  и  b.
Окружность описанная около прямоугольника имеет радиус, равный половине диагонали.
Диагональ по теореме Пифагора
√(a²+b²) 
Площадь части круга красного цвета на рисунке 2
S(красной части)=π(√(a²+b²)/2)²-ab=π(a²+b²)/4 - ab

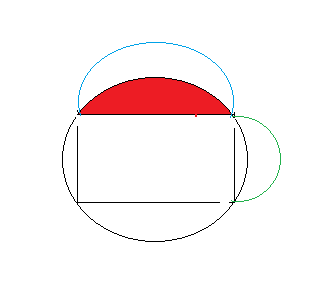
Cм. рисунок 3 в приложении. Полуокружность синего цвета построена на стороне a как на диаметре. Площадь этой полуокружности равна π·(a/2)²:2
Таких полуокружностей две. Снизу и сверху.
Поэтому площадь под двумя синими полуокружностями  π·a²/4
Аналогично полуокружность зелёного цвета построена на стороне b как на диаметре. Площадь этой полуокружности равна π·(b/2)²:2
Таких полуокружностей две. Слева  и справа.
Поэтому получим площадь под двумя зелёными полуокружностями  π·b²/4
Площадь под всеми четырьмя полуокружностями равна
   π·a²/4+π·b²/4 =π·(a² + b²)/4
Вычитаем площадь красной части
π·(a² + b²)/4 - ( π(a²+b²)/4 - ab)= ab  - площадь четырех луночек Гиппократа

и площадь прямоугольника тоже равна ab

Answer 2

С серпами Гиппократа пока не разобралась. Одна дуга окружности понятно как проведена, а вот вторая - нет