Предмет: Алгебра,
автор: micha02204
3^(x^2+1) + 5^(x^4))=4-sin^2x
Помогите, пожалуйста. Буду очень поизнателен хотя бы за какую-нибудь идею, как решать это уравнение. Показательное уравнегие кажется не сложным, за исключением синуса, я даже не знаю, что с ним сделать...
Ответы
Автор ответа:
0
здесь только рассуждать о свойствах функций...
в показателях степени выражения неотрицательные, т.е. наименьшие значения для показателей степени ---это нули,
а чем больше показатель степени,
тем больше значение ф-ции (основания >1), значит слева от равенства
меньшее значение (при х=0) 3^1 + 5^0 = 3+1 = 4
синус ф-ция периодическая и ограниченная, хоть в какую степень ее возводи ---больше 1 она не будет)))
-1 < sin(x) < 1
0 < (sin(x))² < 1
0 > -(sin(x))² > -1
-1 < -(sin(x))² < 0
4-1 < 4-(sin(x))² < 4
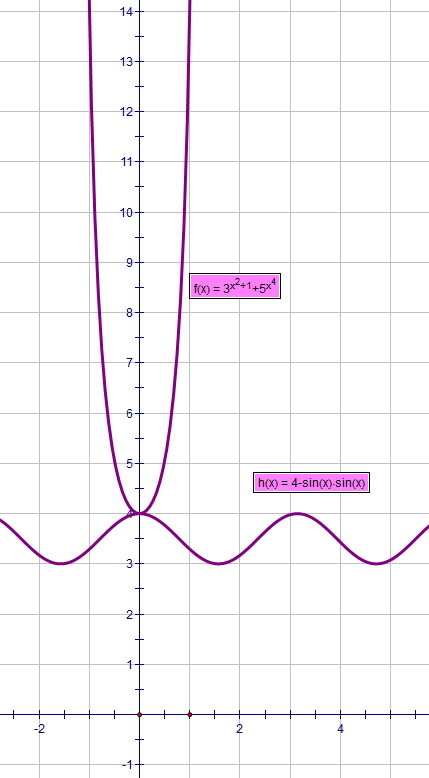
т.е. эти функции "встретиться" могут только в одной точке... при х = 0
это и есть единственное решение...
в показателях степени выражения неотрицательные, т.е. наименьшие значения для показателей степени ---это нули,
а чем больше показатель степени,
тем больше значение ф-ции (основания >1), значит слева от равенства
меньшее значение (при х=0) 3^1 + 5^0 = 3+1 = 4
синус ф-ция периодическая и ограниченная, хоть в какую степень ее возводи ---больше 1 она не будет)))
-1 < sin(x) < 1
0 < (sin(x))² < 1
0 > -(sin(x))² > -1
-1 < -(sin(x))² < 0
4-1 < 4-(sin(x))² < 4
т.е. эти функции "встретиться" могут только в одной точке... при х = 0
это и есть единственное решение...
Приложения:
Автор ответа:
0
уточнение: неравенство для синуса --- нужно было написать знак "меньше или РАВНО"... неточность прокралась)))
Похожие вопросы
Предмет: История,
автор: stuckinurij
Предмет: Английский язык,
автор: zambozovaguldana
Предмет: История,
автор: Ewsivleer
Предмет: Химия,
автор: annaulianovsk
Предмет: Математика,
автор: mbandyuk